
【题目】如图,在平面直角坐标系中,长方形ABCD的顶点B在坐标原点,顶点A、C分别在y轴、x轴的负半轴上,其中![]() ,
,![]() ,将矩形ABCD绕点D逆时针旋转得到矩形
,将矩形ABCD绕点D逆时针旋转得到矩形![]() ,点
,点![]() 恰好落在x轴上,线段
恰好落在x轴上,线段![]() 与CD交于点E,那么点E的坐标为
与CD交于点E,那么点E的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BD,B'D,根据矩形ABCD绕点D逆时针旋转得到矩形A'B'C'D,可得BD=B'D,再根据DC⊥BB',即可得到BC=B'C=2=A'D,再判定△B'EC≌△DEA',得到B'E=DE,设CE=x,则B'E=DE=4x,根据Rt△B'EC中,![]() ,可得
,可得![]() ,求得x的值即可得到点E的坐标.
,求得x的值即可得到点E的坐标.
如图,
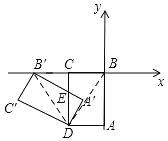
连接BD,B′D,
∵矩形ABCD绕点D逆时针旋转得到矩形A′B′C′D,
∴BD=B′D,
又∵DC⊥BB′,A(0,4),C(2,0),
∴BC=B′C=2=A′D,
又∵∠B′CE=∠DA′E=![]() ,∠B′EC=∠DEA′,
,∠B′EC=∠DEA′,
∴△B′EC≌△DEA′,
∴B′E=DE,
设CE=x,则B′E=DE=4x,
∵Rt△B′EC中![]()
∴![]()
解得x=32,
∴E(2,![]() ),
),
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①,②分别是某吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角. 吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A距地面的高度是多少米?(精确到0.1米. 参考数据:sin10°=cos80°≈0.17,cos10°=sin80°≈0.98,sin20°=cos70°≈0.34,tan70°≈2.75,sin70°≈0.94)
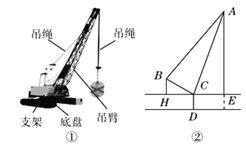
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.
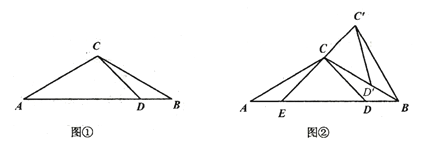
(1)求∠BCD的度数;
(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课外活动,某校决定购买100个篮球和a(a>10)副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)设每个篮球x元,则每副羽毛球拍______元(用含x的代数表示);并求出每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪一家商店购买划算?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
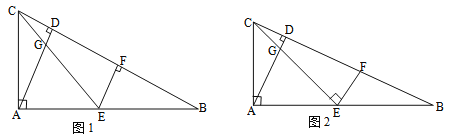
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
(2)如图2,若AC:AB=1: ![]() ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
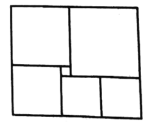
【题目】一个由木条制作的长方形窗户如图所示,里面有6个小正方形,且右下角的正方形的边长比中间最小的正方形的边长多0.4米,若制作这个长方形窗户需要的木条总长至少为a米,则a=________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF,现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当边CD′恰好经过EF的中点H时,求旋转角α的大小;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△BCD′能否全等?若能,直接写出旋转角α的大小;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
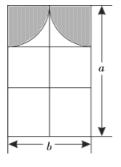
【题目】装修公司给小红家的窗户设计了如图所示的装修方案,上方布料窗眉(阴影部分)由两个半径相同的四分之一圆组成.
(1)分别用整式表示窗眉用布和窗户透光的面积.(窗框的面积忽略不计).
(2)观察(1)中的结果,它们是单项式还是多项式?次数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com