
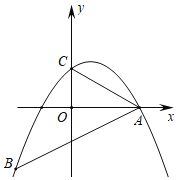
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)求此二次函数的解析式;
(2)证明:AO平分∠BAC;
(3)在二次函数对称轴上是否存在一点P使得AP=BP?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)见解析;(3)存在.点P的坐标为(1,﹣4);
x+2;(2)见解析;(3)存在.点P的坐标为(1,﹣4);
【解析】
(1)将点A(4,0)与点B(4,4)代入函数解析式即可;
(2)求出直线AB的解析式,求出AB与y轴交点D(0,2),可得OC=OD,再由AO⊥CD,可证AO平分∠BAC;
(3)二次函数的对称轴为直线x=1,设点P的坐标为(1,m),AP2=(41)2+m2,BP2=(1+4)2+(m4)2,当AP=BP时,求出m=4即可;
(1)∵点A(4,0)与点B(﹣4,4)在二次函数的图象上,
∴![]() ,
,
解得![]() ,
,
∴二次函数的解析式为y=![]() ;
;
(2)设直线AB的解析式为y=ax+n
则有![]() ,
,
解得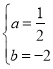 ,
,
故直线AB的解析式为y=![]() x﹣2,
x﹣2,
设直线AB与y轴的交点为点D,
x=0,
则y=﹣2,
故点D为(0,﹣2),
由(1)可知点C为(0,2),
∴OC=OD
又∵AO⊥CD,
∴AO平分∠BAC;
(3)存在.
∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() +2,
+2,
∴二次函数的对称轴为直线x=1,
设点P的坐标为(1,m),
AP2=(4﹣1)2+m2,BP2=(1+4)2+(m4)2,
当AP=BP时,AP2=BP2,
则有9+m2=25+m2+16+8m,
解得m=﹣4,
∴点P的坐标为(1,﹣4);


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
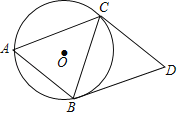
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
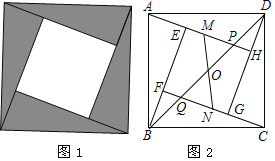
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:
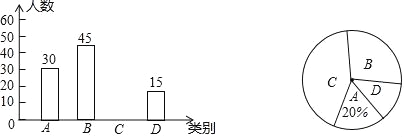
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
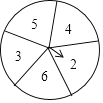
【题目】现有一个如图所示的标有2、3、4、5、6的转盘,另有五张分别标有1、2、3、4、5的扑克,小华和小亮用它们做游戏,先由小华转动转盘一次,记下指针停留时所指的数字;再由小亮随机抽取背面朝上的扑克一张,记下正面的数字.
(1)用列表法或画树状图的方法,求出记下的两个数字之和为8的概率.
(2)若记下的两个数字之和为奇数,则小华得1分;若记下的两个数字之和为偶数,则小亮得1分.这个游戏对双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
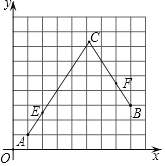
【题目】如图,在下列9×9的网格中,横纵坐标均为整数的点叫做格点,例如:A(1,1)、B(8,3)都是格点,E、F为小正方形边的中点,C为AE、BF的延长线的交点.
(1)AE的长等于 ;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图示所示的网格中,用无刻度的直尺,画出线段PQ,并直接写出P、Q两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,1辆大货车与3辆小货车额定载重量的总和为23吨,2辆大货车与5辆小货车额定载重量的总和为41吨. 1辆大货车、1辆小货车的额定载重量分别为多少吨?设1辆大货车的额定载重量为x吨,1辆小货车的额定载重量为y吨,依题意,可以列方程组为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
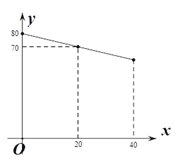
【题目】某果农的苹果园有苹果树60棵,由于提高了管理水平,可以通过补种一些苹果树的方法来提高总产量.但如果多种树,那么树之间的距离和每棵树所受的光照就会减少,单棵树的产量也随之降低.已知在一定范围内,该果园每棵果树产果y(千克)与补种果树x(棵)之间的函数关系如图所示.若超过这个范围,则会严重影响果树的产量.
(1)求y与x之间的函数关系式;
(2)在这个范围内,当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
(3)若该果农的苹果以3元/千克的价格售出,不计其他成本,按(2)的方式可以多收入多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com