
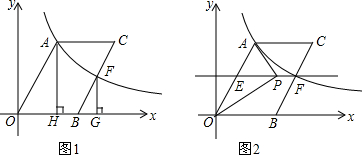
ЗжЮі ЃЈ1ЃЉгЩOA=4ЃЌЁЯAOB=60ЁуЃЌAHЁЭxжсЃЌПЩЧѓЕУAHЃЌOHЕФГЄЃЌМДПЩЧѓЕУЕуAЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУЗДБШР§КЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉгЩAHЁЭxжсЃЌFGЁЭжсЃЌЫФБпаЮOACBЪЧЦНааЫФБпаЮЃЌвзжЄЕУЁїOAHЁзЁїFBGЃЌгжгЩЕуFЮЊBCБпЕФжаЕуЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌЧѓЕУFGЃЌBGЕФГЄЃЌШЛКѓгЩЕуFдкЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЧѓЕУЕуCЕФзјБъЃЌМЬЖјЧѓЕУOGЕФГЄЃЌдђПЩЧѓЕУOBЕФГЄЃЌМЬЖјЧѓЕУЕуCЕФзјБъЃЛ
ЃЈ3ЃЉЙ§ЕуFзїEFЁЮOBЃЌПЩЧѓЕУЕуPЕФзнзјБъЃЌМДПЩЩшЕуPЃЈxЃЌ$\sqrt{3}$ЃЉЃЌМЬЖјПЩЕУPA2=ЃЈx-2ЃЉ2+ЃЈ$\sqrt{3}$-2$\sqrt{3}$ЃЉ2=x2-4x+7ЃЌOP2=x2+ЃЈ$\sqrt{3}$ЃЉ2=x2+3ЃЌOA2=16ЃЌШЛКѓЗжБ№ДгЕБЁЯAPO=90ЁуЪБЃЌдђPA2+OP2=OA2ЃЌЕБЁЯPAO=90ЁуЪБЃЌPA2+OA2=OP2ЃЌЕБЁЯPOA=90ЁуЪБЃЌOP2+OA2=PA2ЃЌШЅЗжЮіЧѓНтМДПЩЧѓЕУД№АИЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпOA=4ЃЌЁЯAOB=60ЁуЃЌAHЁЭxжсЃЌ
ЁрAH=OA•sin60Ёу=4ЁС$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$ЃЌOH=OA•cos60Ёу=4ЁС$\frac{1}{2}$=2ЃЌ
ЁрЕуAЃЈ2ЃЌ2$\sqrt{3}$ЃЉЃЌ
ЁпЗДБШР§КЏЪ§y=$\frac{k}{x}$ЃЈkЃО0ЃЉдкЕквЛЯѓЯоФкЕФЭМЯѓОЙ§ЕуAЃЌ
Ёр2$\sqrt{3}$=$\frac{k}{2}$ЃЌ
НтЕУЃКk=4$\sqrt{3}$ЃЌ
ЁрЗДБШР§КЏЪ§НтЮіЪНЮЊЃКy=$\frac{4\sqrt{3}}{x}$ЃЛ
ЃЈ2ЃЉЁпAHЁЭxжсЃЌFGЁЭжсЃЌ
ЁрЁЯAHO=ЁЯFGB=90ЁуЃЌ
ЁпЫФБпаЮOACBЪЧЦНааЫФБпаЮЃЌ
ЁрOAЁЮBCЃЌOA=BCЃЌ
ЁрЁЯOAH=ЁЯFBGЃЌ
ЁрЁїAOHЁзЁїFBGЃЌ
Ёр$\frac{OA}{BF}=\frac{AH}{FG}=\frac{BG}{OH}$ЃЌ
ЁпЕуFЮЊBCБпЕФжаЕуЃЌ
ЁрBFЃКOA=1ЃК2ЃЌ
ЁрFG=$\frac{1}{2}$AH=$\sqrt{3}$ЃЌBG=$\frac{1}{2}$OH=1ЃЌ
ЁпЕуFдкЗДБШКЏЪ§ЕФЭМЯѓЩЯЃЌ
ЁрЕуFЃЈ4ЃЌ$\sqrt{3}$ЃЉЃЌ
ЁрOG=4ЃЌ
ЁрOC=OG-BG=3ЃЌ
ЁрAC=OB=3ЃЌ
ЁрЕуCЕФзјБъЮЊЃКЃЈ5ЃЌ2$\sqrt{3}$ЃЉЃЛ
ЃЈ3ЃЉДцдкШ§жжЧщПіЃЎ
ЁпEFЁЮOBЃЌ
ЁрЕуPЕФзнзјБъЮЊЃК$\sqrt{3}$ЃЌ
ЩшЕуPЃЈxЃЌ$\sqrt{3}$ЃЉЃЌ
ЁрPA2=ЃЈx-2ЃЉ2+ЃЈ$\sqrt{3}$-2$\sqrt{3}$ЃЉ2=x2-4x+7ЃЌOP2=x2+ЃЈ$\sqrt{3}$ЃЉ2=x2+3ЃЌOA2=16ЃЌ
ЕБЁЯAPO=90ЁуЪБЃЌдђPA2+OP2=OA2ЃЌ
МДx2-4x+7+x2+3=16ЃЌ
НтЕУЃКx1=3ЃЌx2=-1ЃЌ
ЁрP1ЃЈ3ЃЌ$\sqrt{3}$ЃЉЃЌP2ЃЈ-1ЃЌ$\sqrt{3}$ЃЉЃЛ
ЕБЁЯPAO=90ЁуЪБЃЌPA2+OA2=OP2ЃЌ
МДx2-4x+7+16=x2+3ЃЌ
НтЕУЃКx=5ЃЌ
ЁрP3ЃЈ5ЃЌ$\sqrt{3}$ЃЉЃЛ
ЕБЁЯPOA=90ЁуЪБЃЌOP2+OA2=PA2ЃЌ
МДx2-4x+7=16+x2+3ЃЌ
НтЕУЃКx=-3ЃЌ
ЁрP4ЃЈ-3ЃЌ$\sqrt{3}$ЃЉЃЎ
злЩЯПЩЕУЃКЕуPЕФзјБъЮЊЃКP1ЃЈ3ЃЌ$\sqrt{3}$ЃЉЃЌP2ЃЈ-1ЃЌ$\sqrt{3}$ЃЉЃЌP3ЃЈ5ЃЌ$\sqrt{3}$ЃЉЃЌP4ЃЈ-3ЃЌ$\sqrt{3}$ЃЉЃЎ
ЕуЦР ДЫЬтЪєгкЗДБШР§КЏЪ§злКЯЬтЃЌПМВщСЫД§ЖЈЯЕЪ§ЧѓКЏЪ§НтЮіЪНЁЂЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЁЂЙДЙЩЖЈРэвдМАШ§НЧКЏЪ§ЕШжЊЪЖЃЎНтДЫЬтЕФЙиМќЪЧРћгУЗжРрЬжТлЫМЯыгыЗНГЬЫМЯыЧѓНтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
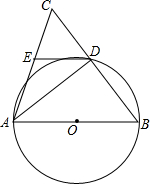 ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯABC=mЁуЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуDЃЌСЌНгADЃЎ
ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯABC=mЁуЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуDЃЌСЌНгADЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
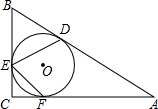 ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=70ЁуЃЌЁїABCЕФФкЧадВЁбOгыБпABЁЂBCЁЂCAЗжБ№ЯрЧагкЕуDЁЂEЁЂFЃЌдђЁЯDEFЕФЖШЪ§ЮЊ80ЁуЃЎ
ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=70ЁуЃЌЁїABCЕФФкЧадВЁбOгыБпABЁЂBCЁЂCAЗжБ№ЯрЧагкЕуDЁЂEЁЂFЃЌдђЁЯDEFЕФЖШЪ§ЮЊ80ЁуЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com