
分析 (1)方程的两个部分具备倒数关系,若设y=x2-x,则原方程另一个分式为12×$\frac{1}{y}$.可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验;(2)方程的两个部分具备倒数关系,若设y=$\frac{{x}^{2}}{x+1}$,则原方程另一个分式为$\frac{1}{y}$.可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
解答 解:(1)y=x2-x,则原方程化为y-12×$\frac{1}{y}$=4,
整理得y2-4y-12=0,
解这个方程,得y1=6,y2=-2.
当y=6时,x2-x=6,即x2-x-6=0,
解这个方程,得x1=-2,x2=3.
当y=-2时,x2-x=-2,即x2-x+2=0,
∵△=1-8<0,∴这个方程没有实数根.
经检验,x1=-2,x2=3都是原方程的根.
∴原方程的根是x1=-2,x2=3;
(2)设y=$\frac{{x}^{2}}{x+1}$,则原方程化为3y-$\frac{1}{y}$=2,
整理得3y2-2y-1=0,
解这个方程,得y1=1,y2=-$\frac{1}{3}$.
当y=1时,$\frac{{x}^{2}}{x+1}$=1,即x2-x-1=0,
解这个方程,得x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
当y=-$\frac{1}{3}$时,$\frac{{x}^{2}}{x+1}$=-$\frac{1}{3}$,即3x2+x+1=0,
∵△=1-12<0,∴这个方程没有实数根.
经检验,x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$都是原方程的根.
∴原方程的根是x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
点评 本题考查了换元法解分式方程,用换元法解分式方程是常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.


科目:初中数学 来源: 题型:选择题
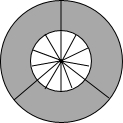 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )| A. | 平移一次形成的 | |
| B. | 平移两次形成的 | |
| C. | 以轴心为旋转中心,旋转120°后形成的 | |
| D. | 以轴心为旋转中心,旋转120°、240°后形成的 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
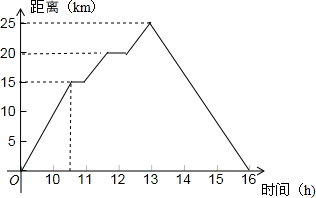 如图所示的图象,表示张同学骑车离家的距离与时间的关系,他9:00离开家,16:00到家,根据图象回答下列问题;
如图所示的图象,表示张同学骑车离家的距离与时间的关系,他9:00离开家,16:00到家,根据图象回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 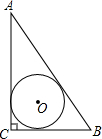 | B. | 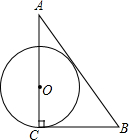 | C. | 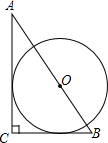 | D. | 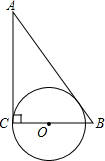 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com