
分析 首先根据题意画出图形,由这个平行四边形的周长为68cm,可得邻边和为34cm,又由两条对角线的长度之比为2:3,可设OA=2xcm,OB=3xcm,然后由两个形状不同的三角形的周长和为80cm,得方程34+4x+3x+3x=80,继而求得答案.
解答 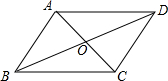 解:如图,∵四边形ABCD是平行四边形,
解:如图,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,AD=BC,
∵这个平行四边形的周长为68cm,
∴AB+BC=34cm,
∵两条对角线的长度之比为2:3,
∴OA:OB=2:3,
设OA=2xcm,OB=3xcm,
根据题意得:34+2OA+OB+OC=80,
即34+4x+3x+3x=80,
解得:x=4.6,
∴OA=9.2cm,OB=13.8cm,
∴AC=18.4cm,BD=27.6cm.
故答案为:18.4cm,27.6cm.
点评 此题考查了平行四边形的性质.注意利用方程思想求解是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
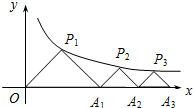 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点P2015的坐标是($\sqrt{2015}$+$\sqrt{2014}$,$\sqrt{2015}$-$\sqrt{2014}$).
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点P2015的坐标是($\sqrt{2015}$+$\sqrt{2014}$,$\sqrt{2015}$-$\sqrt{2014}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
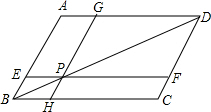 如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.
如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
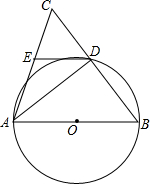 如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.
如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com