练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在锐角三角形ABC中，CM为AB边上的高，P为BC的中点，连接MP，在AC上找到一点N，使NP=MP，连接BN，试判断BN与AC的位置关系，并说明理由．
    考点：直角三角形斜边上的中线
    专题：
    分析：根据直角三角形斜边上的中线等于斜边的一半可得MP=
    1
    2
    BC，然后求出NP=
    1
    2
    BC，再根据直角三角形斜边上的中线等于斜边的一半解答．
    解答：解：BN⊥AC．
    ∵CM为AB边上的高，P为BC的中点，
    ∴MP=
    1
    2
    BC，
    ∵NP=MP，
    ∴NP=
    1
    2
    BC，
    ∴BN⊥AC．
    点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，△ABD中，AB=AD，AC平分∠BAD，交BD于点E．
    （1）求证：△BCD是等腰三角形；
    （2）若∠ABD=50°，∠BCD=130°，求∠ABC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在一个不透明的盒子里装有只有颜色不同的黑、白两种球共5个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
    （1）请估计：当n很大时，摸到白球的频率将会接近
     
    ；（精确到0.1）
    （2）假如你摸一次，求你摸到白球的概率P；
    （3）如果不放回的连续摸两个球，求都摸到白球的概率．（要求画树状图）
    N摸球的次数10020030050080010003000
    M摸到白球的次数651241783024815991803
    m/n摸到白球的概率0.650.620.5930.6040.6010.5990.601

    查看答案和解析>>

    科目：初中数学 来源： 题型：

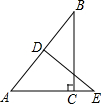    如图，△ABC中，∠ACB=90°，AB=10，BC比AC大2，DE垂直平分AB，交AB于D，交AC的延长线于E．求：
    （1）AC，BC的长；
    （2）CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若x，y是二元一次方程组
    2x+3y=-3
    3x+2y=7
    的解，那么x-y的值是（　　）
    A、10B、4C、3D、2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （-0.4）2015•（
    5
    2
    ）2015=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列运算正确的是（　　）
    A、
    		16
    =±4
    B、
    3(-2)3
    =-2
    C、
    		(-2)2
    =-2
    D、
    		22+32
    =2+3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    方程x（x+4）=x+4的解为（　　）
    A、x=1
    B、x=-4
    C、x1=1，x2=-4
    D、x1=-1，x2=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知∠ABM=90°，AB=AC，过点A作AG丄BC，垂足为G，延长AG交BM于点，过点A作AN∥BM，过点C作EF∥AD，与射线AN、BM分别相交于点F、E
    （1）求证：△BCE∽△AGC；
    （2）点P是射线AD上的一个动点，设AP=x，四边形ACEP的面积是y，若AF=5，AD=
    25
    3
    ．
    ①求y关于x的函数关系式，并写出定义域；
    ②当点P在射线AD上运动时，是否存在这样的点P，使得△CPE的周长为最小？若存在，求出此时y的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案