
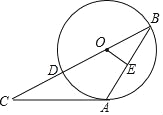
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,且AB=AC,若CD=2![]() ,则OE的长为_____.
,则OE的长为_____.
【答案】![]()
【解析】
连接OA,所以∠OAC=90°,因为AB=AC,所以∠B=∠C,根据圆周角定理可知∠AOD=2∠B=2∠C,故可求出∠B和∠C的度数,在Rt△OAC中,求出OA的值,再在Rt△OAE中,求出OE的值,得到答案.
连接OA,由题意可知∠OAC=90°,∵AB=AC,∴∠B=∠C,,根据圆周角定理可知∠AOD=2∠B=2∠C,∵∠OAC=90°∴∠C+∠AOD=90°,∴∠C+2∠C=90°,故∠C=30°=∠B,∴在Rt△OAC中,sin∠C=![]() =
=![]() ,∴OC=2OA,∵OA=OD,∴OD+CD=2OA,∴CD=OA=2
,∴OC=2OA,∵OA=OD,∴OD+CD=2OA,∴CD=OA=2![]() ,∵OB=OA,∴∠OAE=∠B=30°,∴在Rt△OAE中,sin∠OAE=
,∵OB=OA,∴∠OAE=∠B=30°,∴在Rt△OAE中,sin∠OAE=![]() =
=![]() ,∴OA=2OE,∴OE=
,∴OA=2OE,∴OE=![]() OA=
OA=![]() ,故答案为
,故答案为![]() .
.


科目:初中数学 来源: 题型:
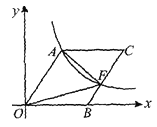
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
A. 10 B. 9 C. 8 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的周长为12,∠A=60°,设边AB的长为x,四边形ABCD的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
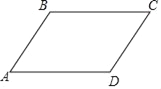
A. 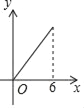 B.
B. 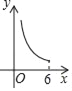 C.
C. 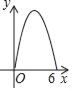 D.
D. 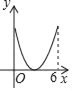
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F.

(1)求证:OE=OF;
(2)如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于![]() BD的所有的等腰三角形.
BD的所有的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
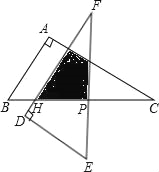
【题目】如图△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.
(1)PH=_____cm.
(2)△ABC与△DEF重叠部分的面积为_____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气候风暴,有极强的破坏力.沿海某城市![]() 的正南方向
的正南方向![]() 的
的![]() 处有一台风中心,其中心风力最大为十二级,每远离台风中心
处有一台风中心,其中心风力最大为十二级,每远离台风中心![]() 千米,风力就减弱一级,该台风中心现在正以
千米,风力就减弱一级,该台风中心现在正以![]() 的速度沿北偏东
的速度沿北偏东![]() 的方向往
的方向往![]() 移动,且台风中心风力不变.若城市所受的风力达到或超过四级,则称为受台风的影响.
移动,且台风中心风力不变.若城市所受的风力达到或超过四级,则称为受台风的影响.
![]() 城市
城市![]() 是否受台风影响?请说明理由;
是否受台风影响?请说明理由;
![]() 如果城市
如果城市![]() 受台风影响,则影响时间有多长?
受台风影响,则影响时间有多长?
![]() 该城市受到台风影响的最大风力为几级?
该城市受到台风影响的最大风力为几级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com