
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+![]() (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.
(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.

科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
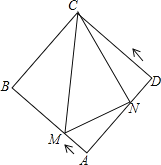
A. 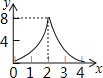 B.
B. 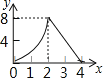
C. 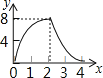 D.
D. 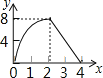
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,过D点作DF⊥AB于点F,
①则cos∠EDF= ;
②求⊙O的半径.
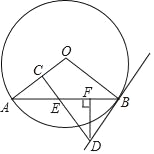
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=6cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以![]() cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
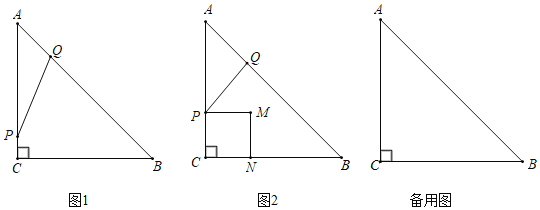
(1)当t=3时,线段PQ的长为 cm;
(2)是否存在某一时刻t,使点B在线段PQ的垂直平分线上?若存在,求出t的值;若不存在,请说明理由;
(3)如图2,以PC为边,往CB方向作正方形CPMN,设四边形CPMN与Rt△ABC重叠部分的面积为S,求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面完全相同的卡片,正面上分别标有数字﹣2,﹣1,1,2.把这四张卡片背面朝上,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com