
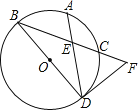
【题目】(本题满分10分)如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.
(1)求证:EF=DF;
(2)若AE=2,ED=4,求EF的长.
【答案】见解析
【解析】解:(1)如图1所示:连接CD.
∵点A是劣弧BC的中点,
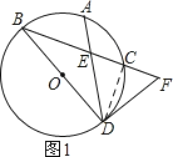
∴弧长AB=弧长AC.
∴∠ADB=∠ADC.
∵BD是圆O的直径,
∴∠DCB=90°.
∴∠CED+∠EDC=90°.
∵DF是圆O的切线,
∴∠BDF=90°.
∴∠EDF+∠BDE=90°.
∴∠FED=∠EDF.
∴EF=DF.
(2)如图2所示:连接AB.
∵点A是劣弧BC的中点,
∴弧长AB=弧长AC.
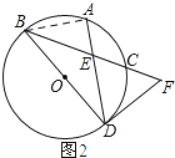
∴∠ADB=∠ABC.
又∵∠A=∠A,
∴△ABE∽△ADB.
∴AB2=AEAD.
∴AB=2![]() .
.
∵BD是圆O的直径,
∴∠DAB=90°.
∴tan∠BDA=tan∠ABC=![]() .
.
∴∠BDA=∠ABC=30°.
∴BD=2AB=4![]() ,∠DBF=30°.
,∠DBF=30°.
∴EF=DF=DB×![]() =4.
=4.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.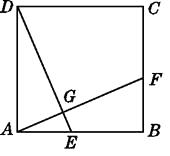
(1)观察图形,写出图中所有与∠AED相等的角;
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某微生物的直径为0.000 005 035m,用科学记数法表示该数为( )
A.5.035×10﹣6
B.50.35×10﹣5
C.5.035×106
D.5.035×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
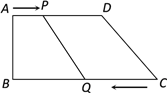
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B = 90,AD = 24厘米,AB = 8厘米,BC = 30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时, 另一点也随之停止运动.
设运动时间为t秒.
(1) 当t在什么时间范围时,CQ>PD?
(2) 存在某一时刻t,使四边形APQB是正
方形吗?若存在,求出t值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com