
【题目】问题一:如图1,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地,若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h), 两车之间距离为y(km).
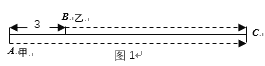
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
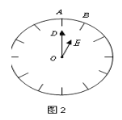
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 km;时针OE指向圆周上的点的速度为每分钟转动 km.
(2)若从2:00起计时,求几分钟后分针与时针第一次重合?
【答案】问题一:(1)1.5h;(2)y=130-60x(2x≤![]() );问题二:(1)6,0.5;(2)
);问题二:(1)6,0.5;(2)![]()
【解析】
问题一:(1)根据两车间的距离=速度之差×时间,即可列出关于x的一元一次方程,然后解方程即可;
(2)分0≤x≤1.5,1.5<x≤2,2<x≤![]() 三种情况找出y关于x的函数关系式;
三种情况找出y关于x的函数关系式;
问题二:(1)运用速度=路程÷时间进行计算即可.;
(2)设经过x分钟后分针和时针第一次重合,根据分针比时针多跑了60km,即可得出关于的一元一次方程,然后解方程即可.
解:问题一:(1)根据题意得:(80-60)x=30,解得:x=1.5.
故答案为:1.5h.
(2)当0<x<1.5时,y=30-(80-60)x=-20x+30;
当1.5 <x<2时,y=80x-(60x+30)=20x-30;
当2<x≤![]() 时,y=160-60x-30=-60x+130
时,y=160-60x-30=-60x+130
∴两车之间的距离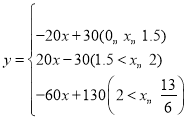
问题二:(1)30÷5=6(km),30÷60=0.5(km);
故答案为:6,0.5.
(2)设经过x分钟后分针和时针第一次重合,
根据题意得:6t-0.5t=30×2.
解得:![]()
答:从2:00起计时,![]() 分钟后分针与B时针第—次重合.
分钟后分针与B时针第—次重合.


科目:初中数学 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粮库6天内发生粮食进、出库的吨数如下(“![]() ”表示进库,“
”表示进库,“![]() ”表示出库):
”表示出库):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)经过这6天,库里的粮食是增多还是减少了?增加(减少)了多少?
(2)经过这6天,管理员结算时发现库里还存480吨粮,那么6天前库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况,并统计绘制成了如图两幅不完整的条形统计图和扇形统计图,请根据所提供的信息,解答下列问题:
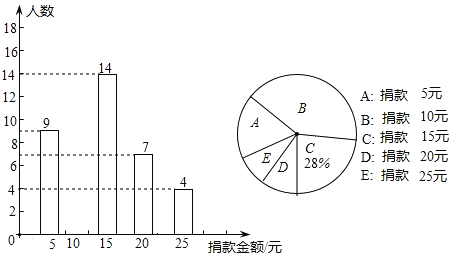
(1)本次共抽查学生 人,并将条形图补充完整:
(2)捐款金额的众数是 元,中位数是 元;
(3)若该校共有2000名学生参加捐款,根据样本平均数估计该校大约可捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明爸爸带着小明和小明弟弟去离家66 千米的外婆家,小明爸爸有一辆摩托车,只坐一人时速度为50 千米/小时,坐两人时速度为 40 千米/小时(交通法规定:摩托车最多只能坐两人)。小明和小明弟弟如果步行速度均为10千米/小时,为尽快达到外婆家,出发时,小明步行,小明爸爸将小明弟弟载了一段路程后让其步行前往外婆家,并立即返回接步行的小明,再到外婆家,结果与小明弟弟同时到达外婆家,则小明从家到外婆家步行的时间为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了 20 天内生产1200 台GH 型电子产品的总任务。已知每台GH 型产品由 4 个G 型装 置和3 个 H 型装置配套组成。工厂现有80 名工人,每个工人每天能加工6 个G 型装置或3 个 H 型装置。工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G 、H 型装置数量正好组成GH 型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH 型电子产品?
(2)工厂补充 40名新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工 4个G型装置,则补充新工人后每天能配套生产多少产品?补充新工人后20天内能完成总任务吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
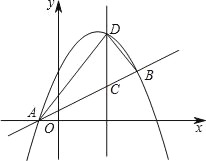
【题目】如图,抛物线y=ax2+bx+![]() 与直线AB交于点A(﹣1,0),B(4,
与直线AB交于点A(﹣1,0),B(4,![]() ),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)求抛物线的表达式;
(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE∥BF,CE=BF.则添加下列条件还不能使△EAC≌△FDB.( )

A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com