
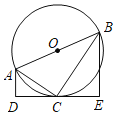
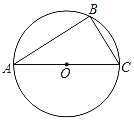
【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=![]() ,CE=3,则
,CE=3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() πC.
πC.![]() πD.
πD.![]() π
π
【答案】D
【解析】
连接OC,由AB是⊙O的直径得到∠ACB=90°,由此证得∠DAC=∠ECB,再证△ADC∽△CEB,列对应边成比例由此求出∠ABC=30°,根据直线DE与⊙O相切于点C求出∠ACD=∠ABC=30°求出AB得到半径,再利用弧长公式计算.
解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,BE⊥DE,
∴∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB,
∴![]() ,即
,即![]() ,
,
∵tan∠ABC=![]() ,
,
∴∠ABC=30°,
∴AB=2AC,∠AOC=60°,
∵直线DE与⊙O相切于点C,
∴∠ACD=∠ABC=30°,
∴AC=2AD=2![]() ,
,
∴AB=4![]() ,
,
∴⊙O的半径为2![]() ,
,
∴![]() 的长为:
的长为:![]() =
=![]() π,
π,
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
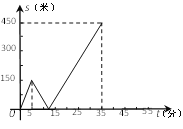
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小涛根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
请直接写出:![]() =, m=, n=;
=, m=, n=;
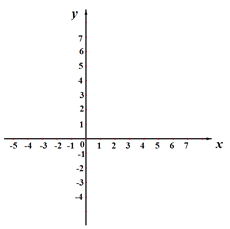
(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数![]() 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)
(4)请结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,直接写出
有三个不同的解,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
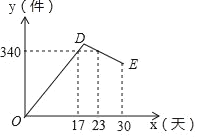
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2![]() .
.
(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年3月16日,由中国科协主办的第六届全国青年科普创新实验暨作品大赛启动,重点围绕“智能、环保、教育”三大主题,某中学派出甲、乙两组队伍参加本次大赛,有四个命题供他们选择:
①智能:智能控制及人工智能命题(用![]() 表示)
表示)
②环保:包括生物环境、风能两个命题(分别用![]() 表示)
表示)
③教育:未来教育命题(用![]() 表示)
表示)
![]() 甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
![]() 若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com