
【题目】已知:数轴上A、B两点表示的有理数分别为a、b,且(a﹣1)2+|b+2|=0
(1)求(a+b)2017的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.
![]()
【答案】(1)﹣1;(2)﹣4或3.
【解析】试题分析:
(1)由已知条件可得![]() 的值,代入
的值,代入![]() 中计算即可;
中计算即可;
(2)由(1)可知A、B两点间的距离为3,因此点C不在A、B之间,可分点C在A的右侧和点C在B的左侧两种情形结合图形讨论即可得到答案.
试题解析:
(1)∵(a﹣1)2+|b+2|=0,
∴ a﹣1=0,b+2=0,
解得a=1,b=﹣2,
∴(a+b)2017=(1﹣2)2017=(﹣1)2017=﹣1;
(2)∵a=1,b=﹣2,数轴上A、B两点表示的有理数分别为a、b,数轴上的点C与A、B两点的距离的和为7,
∴点C可能在点B的左侧或点C可能在点A的右侧,
当点C在点B的左侧时,1﹣c+﹣2﹣c=7,得c=﹣4,
当点C在点A的右侧时,c﹣1+c﹣(﹣2)=7,得c=3.


科目:初中数学 来源: 题型:
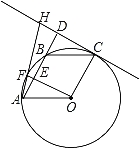
【题目】(2016湖北省荆州市第23题)如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=6﹣3![]() ,求EF和半径OA的长.
,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足![]() +(c-8)2=0.
+(c-8)2=0.
![]()
(1) a = ,b = ,c = .
(2) 若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4) 请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.

(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】团队游客年龄的方差分别是S甲2=1.4,S乙2=18.8,S丙2=2.5,导游小力最喜欢带游客年龄相近龄的团队,则他在甲、乙、丙三个的中应选_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥百大集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,才能使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家把1,3,6,10,15,21叫做三角数,它有一定的规律性,若把第一个三角数记为a1,第二个三角数记为a2,, 第n个三角数记为an,计算a1+a2,a2+a3,a3+a4,,由此推算a199+a200的值为( )
A. 20000 B. 40000 C. 39701 D. 19701
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com