
【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.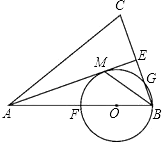
(1)求证:AE与⊙O相切;
(2)当BC=4,AC=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,并阅读相关文字.
![]()
2条直线相交,3条直线相交,4条直线相交,5条直线相交;
有2对对顶角,有6对对顶角,有12对对顶角,有20对对顶角;
通过阅读分析上面的材料,计算后得出规律,当n条直线相交于一点时,有多少对对顶角出现(n为大于2的整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在同一直线上,△ABD和△BCE都是等边三角形,AE,CD分别与BD,BE交于点F,G,连接FG,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG;④AD⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,AB∥ED ,交BC于E,交 AC于F, DE = BC,![]() .
.

(1) 求证:△FCD 是等腰三角形
(2) 若AB=3.5cm,求CD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,连接
,连接![]() 、
、![]() .
.

(1)若![]() ,判断
,判断![]() _______
_______![]() (填“
(填“![]() ,
,![]() 或
或![]() ”)
”)
(2)当![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() ______时,
______时,![]() 是等腰三角形.(请直接写出答案)
是等腰三角形.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.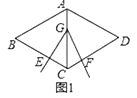
(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;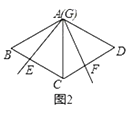
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若 ![]() =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);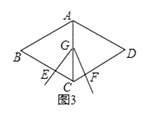
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF= ![]() ,当t>2时,求EC的长度.
,当t>2时,求EC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△AB C沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
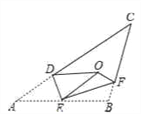
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com