
【题目】如图,点A,B,C在同一直线上,△ABD和△BCE都是等边三角形,AE,CD分别与BD,BE交于点F,G,连接FG,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG;④AD⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)

【答案】①②③⑤
【解析】
易证△ABE≌△DBC,则有∠BAE=∠BDC,AE=CD,从而可证到△ABF≌△DBG,则有AF=DG,BF=BG,由∠FBG=60°可得△BFG是等边三角形,证得∠BFG=∠DBA=60°,则有FG∥AC,由∠CDB≠30°,可判断AD与CD的位置关系.
∵△ABD和△BCE都是等边三角形,∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°.
∵点A、B、C在同一直线上,∴∠DBE=180°﹣60°﹣60°=60°,∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,∵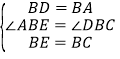 ,∴△ABE≌△DBC,∴∠BAE=∠BDC,∴AE=CD,∴①正确;
,∴△ABE≌△DBC,∴∠BAE=∠BDC,∴AE=CD,∴①正确;
在△ABF和△DBG中,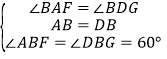 ,∴△ABF≌△DBG,∴AF=DG,BF=BG.
,∴△ABF≌△DBG,∴AF=DG,BF=BG.
∵∠FBG=180°﹣60°﹣60°=60°,∴△BFG是等边三角形,∴∠BFG=60°,∴②正确;
∵AE=CD,AF=DG,∴EF=CG;∴③正确;
∵∠ADB=60°,而∠CDB=∠EAB≠30°,∴AD与CD不一定垂直,∴④错误.
∵△BFG是等边三角形,∴∠BFG=60°,∴∠GFB=∠DBA=60°,∴FG∥AB,∴⑤正确.
故答案为:①②③⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= . 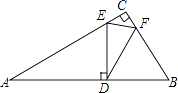
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则下列结论错误的是( )
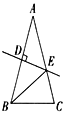
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
(1)试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)若∠BOC=60°,求∠AOD的度数;
(3)猜想∠AOD与∠BOC在数量上是相等,互余,还是互补的关系,并说明理由;
(4)当∠COD绕着点O旋转到图(2)所示位置时,你在(3)中的猜想还成立吗?请用你所学的知识加以说明.
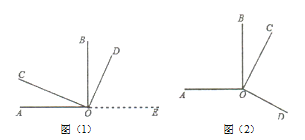
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线OD交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC度数为( ).

A. 108° B. 135° C. 144° D. 160°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com