
【题目】如图(1)所示,∠AOB、∠COD都是直角.
(1)试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)若∠BOC=60°,求∠AOD的度数;
(3)猜想∠AOD与∠BOC在数量上是相等,互余,还是互补的关系,并说明理由;
(4)当∠COD绕着点O旋转到图(2)所示位置时,你在(3)中的猜想还成立吗?请用你所学的知识加以说明.
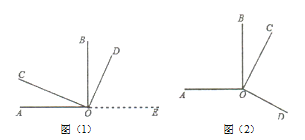
【答案】(1)![]() ,理由详见解析;(2)120°;(3)
,理由详见解析;(2)120°;(3)![]() ,理由详见解析;(4)
,理由详见解析;(4)![]() 成立,理由详见解析.
成立,理由详见解析.
【解析】
(1)根据角的和差可以求得∠AOC、∠BOD的大小关系.
(2)根据角的和差求出∠AOC和∠AOD的度数即可;
(3)根据直角的定义可得∠AOB=∠COD=90°,然后用∠AOD和∠COB表示出∠BOD,列出方程整理即可得解;
(4)根据周角等于360°列式整理即可得解.
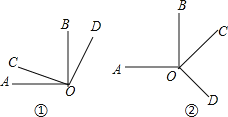
(1)如图①,相等,理由如下:
∵∠AOB、∠COD都是直角,∴∠AOB=∠COD=90°,∴∠AOB﹣∠BOC=∠COD﹣∠BOC,即∠AOC=∠BOD;
(2)∵∠BOC=60°,∠AOB=90°,∴∠AOC=∠AOB-∠BOC =90°-60°=30°.
∵∠COD=90°,∴∠AOD=∠COD+∠AOC= 90°+30°=120°.
(3)∠AOD与∠COB互补.理由如下:
∵∠AOB、∠COD都是直角,∴∠AOB=∠COD=90°,∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°,∠BOD=∠COD﹣∠COB=90°﹣∠COB,∴∠AOD﹣90°=90°﹣∠COB,∴∠AOD+∠COB=180°,∴∠AOD与∠COB互补;
(4)成立.理由如下:
∵∠AOB、∠COD都是直角,∴∠AOB=∠COD=90°.
∵∠AOB+∠BOC+∠COD+∠AOD=360°,∴∠AOD+∠COB=180°,∴∠AOD与∠COB互补.


科目:初中数学 来源: 题型:
【题目】已知,点A,点B分别在线段MN,PQ上∠ACB﹣∠MAC=∠CBP
(1)如图1,求证:MN∥PQ;
(2)分别过点A和点C作直线AG、CH使AG∥CH,以点B为顶点的直角∠DBI绕点B旋转,并且∠DBI的两边分别与直线CH,AG交于点F和点E,如图2试判断∠CFB、∠BEG是之间的数量关系,并证明;
(3)在(2)的条件下,若BD和AE恰好分别平分∠CBP和∠CAN,并且∠ACB=60°,求∠CFB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在同一直线上,△ABD和△BCE都是等边三角形,AE,CD分别与BD,BE交于点F,G,连接FG,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG;④AD⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,连接
,连接![]() 、
、![]() .
.

(1)若![]() ,判断
,判断![]() _______
_______![]() (填“
(填“![]() ,
,![]() 或
或![]() ”)
”)
(2)当![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() ______时,
______时,![]() 是等腰三角形.(请直接写出答案)
是等腰三角形.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.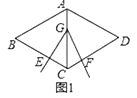
(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;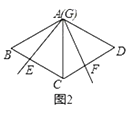
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若 ![]() =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);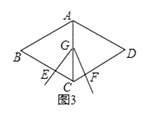
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF= ![]() ,当t>2时,求EC的长度.
,当t>2时,求EC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
![]()
![]()
![]()
![]()
![]()
![]()
如图,在上面的数据中,用一个长方形圈出同一列的三个数,这列的第一个数表示为![]() ,其余各数分别用a、
,其余各数分别用a、![]() 表示:
表示:
(1)若这三个数分别在这三行数的第![]() 列,请用含
列,请用含![]() 的式子分别表示
的式子分别表示![]() 的值;
的值;
(2)若![]() 记为
记为![]() 求
求![]() 这三个数的和(结果用含
这三个数的和(结果用含![]() 的式子表示并化简).
的式子表示并化简).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com