Question

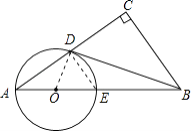
【题目】如图，在Rt△ABC中，∠C=90°，点D是AC的中点，且∠A+∠CDB=90°，过点A，D作⊙O，使圆心O在AB上，⊙O与AB交于点E．

（1）求证：直线BD与⊙O相切；
（2）若AD：AE= ： ，BC=6，求切线BD的长．

Answer 1

【答案】
（1）证明：连接OD
∵OA=OD，

∴∠A=∠ADO（等边对等角）．

又∵∠A+∠CDB=90°（已知），

∴∠ADO+∠CDB=90°（等量代换），

∴∠ODB=180°﹣（∠ADO+∠CDB）=90°，即BD⊥OD．

又∵OD是圆O的半径．

∴BD是⊙O切线

（2）解：连接DE，则∠ADE=90°（圆周角定理）．

∵∠C=90°，

∴∠ADE=∠C，

∴DE∥BC，

又∵D是AC中点，

∴DE是△ABC的中位线，

∴DE= BC=3，AE=BE．

∵AD：AE= ： ，

在直角△ADE中，利用勾股定理求得AE=3 ，则AB=6 ．

∴BD2=ABBE=6 ×3 =54，

∴BD=3 ．

【解析】（1）要证明BD是⊙O切线，由题意可知点D在圆上，因此连接OD，需证OD⊥BD，就要证∠ODB=90°，根据已知易证∠ADO+∠CDB=90°，即可证得结论
（2）先证明DE∥BC，由D是AC中点，可证得DE是△ABC的中位线，即可求得DE的长，再根据AD与AE的比值及勾股定理，就可以求得AE、AB的长，然后根据切割线定理得出BD2=ABBE，从而可求得BD的长。
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．