
���� ��1����22+32��42�����ɵó����ۣ�
��2��������������ٵ�xΪб��ʱ���ڵ�xΪֱ�DZ�ʱ��б��Ϊ4���ɹ��ɶ����������x��ֵ��
��3���ɹ��ɶ������涨�����ɵó����ۣ�
��� �⣺��1����һ�������ε������߳��ֱ���2��3��4������������Ƕ۽������Σ��������£�
��22+32��42��
����������Ƕ۽������Σ�
�ʴ�Ϊ���۽ǣ�
��2����һ�������ε������߳��ֱ���3��4��x�������������ֱ�������Σ�
��x��ֵΪ5��$\sqrt{7}$���������£�
�����������
�ٵ�xΪб��ʱ��x=$\sqrt{{3}^{2}+{4}^{2}}$=5��
�ڵ�xΪֱ�DZ�ʱ��б��Ϊ4��x=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$��
����������x��ֵΪ5��$\sqrt{7}$��
�ʴ�Ϊ��5��$\sqrt{7}$��
��3����һ�������ε������߳��ֱ���$\frac{{{m^2}-{n^2}}}{2}$��mn��$\frac{{{m^2}+{n^2}}}{2}$�������������ֱ�������Σ��������£�
��$\frac{{m}^{2}+{n}^{2}}{2}$��$\frac{{m}^{2}-{n}^{2}}{2}$��$\frac{{m}^{2}+{n}^{2}}{2}$��mn��${��{\frac{{{m^2}-{n^2}}}{2}}��^2}+{��{mn}��^2}$=${��{\frac{{{m^2}+{n^2}}}{2}}��^2}$��
�������������ֱ�������Σ�
���� ���⿼���˹��ɶ������涨�����������չ��ɶ������涨�������ܼ���������֤������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
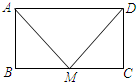 ��ͼ����֪��MΪ����ABCD�б�BC���е㣬��Ҫʹ��AMDΪ����ֱ�������Σ�����������һ��������ô�����и����������У�������ǣ�������
��ͼ����֪��MΪ����ABCD�б�BC���е㣬��Ҫʹ��AMDΪ����ֱ�������Σ�����������һ��������ô�����и����������У�������ǣ�������| A�� | ��AMD=90�� | B�� | AM�ǡ�BAD��ƽ���� | ||
| C�� | AM��AD=1��$\sqrt{2}$ | D�� | AB��BC=1��$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
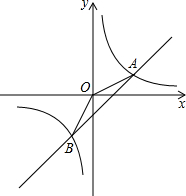 ��ͼ����֪����������y1=$\frac{k}{x}$��kΪ������k��0����ͼ����һ�κ���y2=mx+n ��m��0�����ڵ�A��2��3������B��-1��a����
��ͼ����֪����������y1=$\frac{k}{x}$��kΪ������k��0����ͼ����һ�κ���y2=mx+n ��m��0�����ڵ�A��2��3������B��-1��a�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
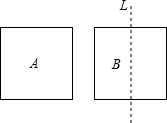 ��������2�ű߳�����2��������ֽƬA��B�����㽫ֽƬA��һ�ߵ�һ���˵����ֽƬB�ĶԳ���L�ϣ���һ���˵���ֽƬB��һ�������غϺ�ѹƽ����ֽƬA��ֽƬB�غϲ��ֵ������
��������2�ű߳�����2��������ֽƬA��B�����㽫ֽƬA��һ�ߵ�һ���˵����ֽƬB�ĶԳ���L�ϣ���һ���˵���ֽƬB��һ�������غϺ�ѹƽ����ֽƬA��ֽƬB�غϲ��ֵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
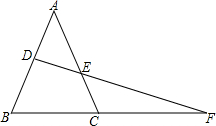 ��ͼ���ڡ�ABC�У�DΪAB���е㣬DF��AC��E����BC���ӳ�����F����֤��AE•CF=BF•EC��
��ͼ���ڡ�ABC�У�DΪAB���е㣬DF��AC��E����BC���ӳ�����F����֤��AE•CF=BF•EC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com