
【题目】已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中∠E=60°,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论:
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )

A. 甲、乙都对 B. 乙对甲不对
C. 甲对乙不对 D. 甲、乙都不对
 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
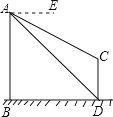
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
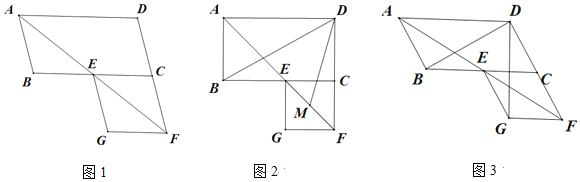
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
调查结果统计表

调查结果频数分布直方图 调查结果扇形统计图

请根据以上图表,解答下列问题:
(1)填空:这次调查的样本容量是 ,![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(4)该校共有![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 的边OB上的一点。
的边OB上的一点。
过点P画OA的垂线,垂足为H;
过点P画OB的垂线,交OA于点C;
线段PH的长度是点P到 的距离,_____ 是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
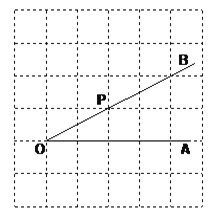
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求点D到AB的距离
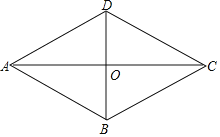
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD//BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)DAE 和CFE全等吗?说明理由;
(2)若AB BCAD,说明 BE AF;
(3)在(2)的条件下,若CE 5,D 90 ,求出E到AB的距离.
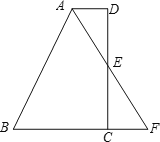
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形![]() 中,
中,![]() .
.
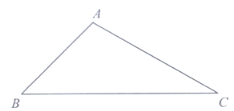
(1)按下列要求画出相应的图形
①过点![]() 画直线
画直线![]() ;
;
②过点![]() 分别画直线
分别画直线![]() 和直线
和直线![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(2)在(1)所画出的图形中,按要求完成下列问题.
①线段____________的长度是点![]() 到
到![]() 的距离,线段
的距离,线段![]() 的长度是点_______到直线__________的距离;
的长度是点_______到直线__________的距离;
②在线段![]() 、
、![]() 、
、![]() 、
、![]() 中,长度最短的是线段___________,理由是:直线外一点与直线上各点连接的所有线段中,________________最短;
中,长度最短的是线段___________,理由是:直线外一点与直线上各点连接的所有线段中,________________最短;
③延长![]() 至点
至点![]() ,试说明
,试说明![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com