
分析 作辅助线,根据切线性质得出O1C⊥CD,O2D⊥CD、O1E⊥FM,O2F⊥FM,则O1E∥O2F和PH∥O2D,
根据平行线分线段成比例定理列比例式求出PG、PH的长,再根据内公切线公式和外公切线公式求出AB和CD的长,从而得出ND、MC的长,根据面积公式代入计算求面积即可.
解答 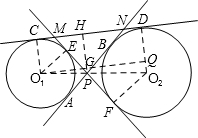 解:设外公切线的两个切点分别为C、D,内公切线的四个切点分别为A、E、B、F,连接O1C、O2D、O1E、O2F,则O1C⊥CD,O2D⊥CD、O1E⊥FM,O2F⊥FM,
解:设外公切线的两个切点分别为C、D,内公切线的四个切点分别为A、E、B、F,连接O1C、O2D、O1E、O2F,则O1C⊥CD,O2D⊥CD、O1E⊥FM,O2F⊥FM,
过P作PH⊥CD于H,过O1作O1Q⊥O2D于Q,两垂线交于点G,连接O1O2,则O1、O2经过点P;
∵O1E⊥FM,O2F⊥FM,
∴O1E∥O2F,
∴$\frac{{O}_{1}P}{{O}_{2}P}$=$\frac{{O}_{1}E}{{O}_{2}F}$=$\frac{3}{5}$,
∵PH⊥CD,O2D⊥CD,
∴PH∥O2D,
∴$\frac{PG}{{O}_{2}Q}$=$\frac{{O}_{1}P}{{O}_{1}{O}_{2}}$=$\frac{3}{8}$,
∴$\frac{PG}{5-3}=\frac{3}{8}$,
∴PG=$\frac{3}{4}$,
∴PH=3+$\frac{3}{4}$=$\frac{15}{4}$,
∵AN=CN,
即AB+BN=CN,
∵CD=CN+DN,
∴CD=AB+BN+ND,
∵ND=BN,
∴BN=ND=$\frac{CD-AB}{2}$,
∵CD=O1Q=$\sqrt{1{0}^{2}-(5-3)^{2}}$=4$\sqrt{6}$,
AB=$\sqrt{1{0}^{2}-(5+3)^{2}}$=6,
∴ND=$\frac{4\sqrt{6}-6}{2}$=2$\sqrt{6}$-3,
同理得:CM=2$\sqrt{6}$-3,
∴MN=CD-CM-ND=4$\sqrt{6}$-2(2$\sqrt{6}$-3)=6,
∴S△PMN=$\frac{1}{2}$MN•PH=$\frac{1}{2}$×6×$\frac{15}{4}$=$\frac{45}{4}$,
故答案为:$\frac{45}{4}$.
点评 本题考查了相离两圆的外公切线和内公切线的性质,首先要确定其所成的三角形,根据面积公式求两边MN和FH的长,因此要熟练掌握圆的切线垂直于经过切点的半径,同时运用了平行线分线段成比例定理和勾股定理求边的长,代入面积公式即可得出结论.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直角三角形的直角顶点放在点A(2,2)处,两直角边分别交x轴、y轴于B、C两点.
如图,在平面直角坐标系中,直角三角形的直角顶点放在点A(2,2)处,两直角边分别交x轴、y轴于B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )| A. | (a-3,b) | B. | (a+3,b) | C. | (3-a,-b) | D. | (a-3,-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com