
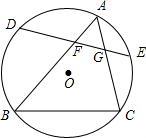
 如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.
如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
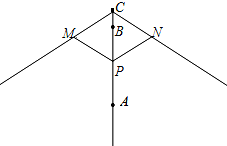 如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )| A. | 四边形PNCM可能会出现为正方形 | B. | 四边形PNCM的周长始终不变 | ||
| C. | 当∠CPN=60°时,CP=AP | D. | 四边形PNCM的面积始终不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
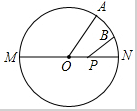 如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.
如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com