
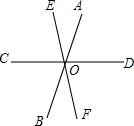
 如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.
如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )
一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )| A、4 | B、4.5 | C、8 | D、9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据:
合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com