练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知直线l与半径为2的⊙O的位置关系是相离，则点O到直线l的距离的取值范围在数轴上的表示正确的是（　　）
    A、
    B、
    C、
    D、
    考点：直线与圆的位置关系,在数轴上表示不等式的解集
    专题：
    分析：根据圆O的半径和圆心O到直线l的距离的大小，相交：d＜r；相切：d=r；相离：d＞r；可求出点O到直线l的距离的取值范围，进而得到答案．
    解答：解：∵l与半径为2的⊙O的位置关系是相离，
    ∴点O到直线l的距离的取值范围d＞2．
    故选A．
    点评：本题考查直线与圆位置关系的定义，①当直线与圆心的距离小于半径，直线与圆相交；②当直线与圆心的距离大于半径，直线与圆相离，③当直线与圆心的距离等于半径，直线与圆相切．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，BC=2，AC=
    		6
    ，AB=
    		3
    +1    ，求△ABC各内角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，OA⊥BC于点O，OD平分∠AOB，OE平分∠DOC，求∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，在△ABC中，已知∠C＞∠B，AD⊥BC于点D，AE平分∠BAC，判断∠EAD与
    1
    2
    （∠C-∠B）的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，AB=AC，AD是BC边上的高，点E，F是AD上的任意两点，若△ABC的面积为10cm2，则图中阴影部分的面积是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

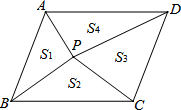    如图，点P是平行四边形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
    ①S1+S3=S2+S4；②若S3=S1，则S4=3S2；③若S1=S4，则S2=2S3；④若S1-S2=S3-S4，能判断P点一定在对角线BD上的正确结论的序号是
     
    （把所有正确结论的序号都填在横线上）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    四边形ABCD是正方形，圆心角等于90°，OE=OF=10，问：正方形边长多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线AB，CD，EF相交于点O，∠AOE：∠AOD=1：3，∠COB：∠DOF=3：4，求证，CD⊥EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，三个村庄A，B，C之间的距离分别为BC=5km，AC=12km，AB=13km．现准备从C村修一条公路CD直达公路AB，已知公路的造价为39000元/km，求修这条公路的最低造价是多少？

    查看答案和解析>>

    同步练习册答案