
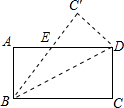
 已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.
已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.分析 (1)先看两三角形中已知的条件有哪些:一组直角(∠A,∠C'),一组对顶角(∠AEB,∠CED),AB=C'D,因此就构成了两三角形全等的条件(AAS);
(2)根据(1)可知∠ABE=∠EDC′,∠C′=90°,得到∠DEC′的度数,易证∠BDE=∠EBD,从而求出∠BDC′的度数.
解答 证明:(1)由题意知,∠A=∠C=∠C′=90°,AB=CD=C′D,
在△ABE和△C′DE中
$\left\{\begin{array}{l}{∠C=∠C′}\\{∠AEB=∠C′ED}\\{AB=C′D}\end{array}\right.$
∴△ABE≌△C′DE.
(2)∴△ABE≌△C′DE,
∴EB=ED,∠ABE=∠EDC′=28°,
∵∠C′=90°,
∴∠C′ED=62°,
∴∠BDE=∠EBD=31°,
∴∠BDC′=90°-∠EBD=59°.
点评 本题考查了全等三角形的判定和性质,通过全等三角形来得出简单的线段相等是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 220 | B. | 218 | C. | 216 | D. | 209 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
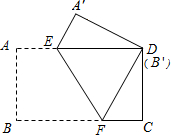 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
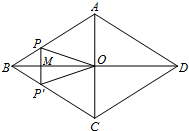 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )| A. | 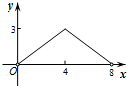 | B. | 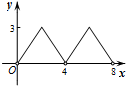 | C. | 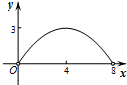 | D. | 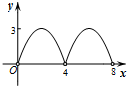 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
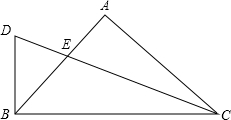 如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
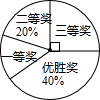 国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com