
分析 (1)用树状图法展示所有9种等可能的结果数;
(2)根据一次函数图象上点的坐标特征,从9个点中找出满足条件的点,然后根据概率公式计算;
(3)利用点与圆的位置关系找出圆上的点和圆外的点,由于过这些点可作⊙O的切线,则可计算出过点M(x,y)能作⊙O的切线的概率.
解答 解:(1)画树状图: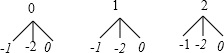
共有9种等可能的结果数,它们是:(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0);
(2)在直线y=-x+1的图象上的点有:(1,0),(2,-1),
所以点M(x,y)在函数y=-x+1的图象上的概率=$\frac{2}{9}$;
(3)在⊙O上的点有(0,-2),(2,0),在⊙O外的点有(1,-2),(2,-1),(2,-2),
所以过点M(x,y)能作⊙O的切线的点有5个,
所以过点M(x,y)能作⊙O的切线的概率=$\frac{5}{9}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了一次函数图象上点的坐标特征和切线的性质.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+2>n+2 | B. | 2m>2n | C. | $\frac{m}{2}$>$\frac{n}{2}$ | D. | m2>n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 目的地 车型 | A村(元/辆) | B村(元/辆) |
| 大货车 | 800 | 900 |
| 小货车 | 400 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
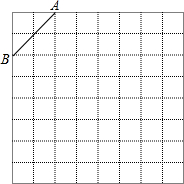 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
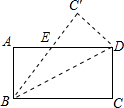 已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.
已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
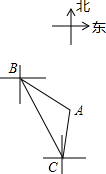 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | $\frac{20\sqrt{3}}{3}$海里 | D. | $\frac{40\sqrt{3}}{3}$海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com