
分析 (1)根据“和谐数”的定义(把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同)写出四个“和谐数”,设任意四位“和谐数”形式为:$\overline{abcd}$,根据和谐数的定义得到a=d,b=c,则 $\frac{\overline{abcd}}{11}$=$\frac{1000a+100b+10c+d}{11}$=$\frac{1000a+100b+10b+a}{11}$=91a+10b为正整数,易证得任意四位“和谐数”都可以被11整除;
(2)设能被11整除的三位“和谐数”为:$\overline{xyz}$,则$\frac{\overline{xyz}}{11}$=$\frac{101x+10y}{11}$=$\frac{99x+11y+2x-y}{11}$=9x+y+$\frac{2x-y}{11}$为正整数.故y=2x(1≤x≤4,x为自然数).
解答 解:(1)四位“和谐数”:1221,1331,1111,6666…(答案不唯一)
任意一个四位“和谐数”都能被11整除,理由如下:
设任意四位“和谐数”形式为:$\overline{abcd}$,则满足:
最高位到个位排列:a,b,c,d.
个位到最高位排列:d,c,b,a.
由题意,可得两组数据相同,则:a=d,b=c,
则 $\frac{\overline{abcd}}{11}$=$\frac{1000a+100b+10c+d}{11}$=$\frac{1000a+100b+10b+a}{11}$=91a+10b为正整数.
∴四位“和谐数”能被11整数,
又∵a,b,c,d为任意自然数,
∴任意四位“和谐数”都可以被11整除;
(2)设能被11整除的三位“和谐数”为:$\overline{xyz}$,则满足:
个位到最高位排列:x,y,z.
最高位到个位排列:z,y,x.
由题意,两组数据相同,则:x=z,
故 $\overline{xyz}$=$\overline{xyx}$=101x+10y,
故$\frac{\overline{xyz}}{11}$=$\frac{101x+10y}{11}$=$\frac{99x+11y+2x-y}{11}$=9x+y+$\frac{2x-y}{11}$为正整数.
故y=2x(1≤x≤4,x为自然数).
点评 本题考查了因式分解的应用.解题的关键是弄清楚“和谐数”的定义,从而写出符合题意的数.


科目:初中数学 来源: 题型:选择题
| A. | a0=1 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a${\;}^{\frac{1}{2}}$=$\frac{1}{{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 220 | B. | 218 | C. | 216 | D. | 209 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
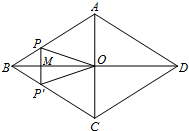 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )| A. | 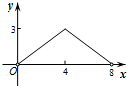 | B. | 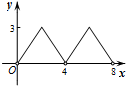 | C. | 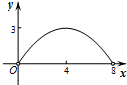 | D. | 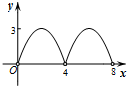 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com