
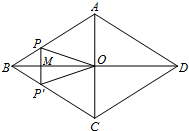
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )| A. | 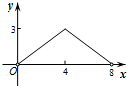 | B. | 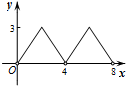 | C. | 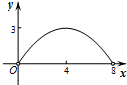 | D. | 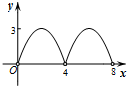 |
分析 由菱形的性质得出AB=BC=CD=DA,OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=4,AC⊥BD,分两种情况:
①当BM≤4时,先证明△P′BP∽△CBA,得出比例式$\frac{PP′}{AC}=\frac{BM}{OB}$,求出PP′,得出△OPP′的面积y是关于x的二次函数,即可得出图象的情形;
②当BM≥4时,y与x之间的函数图象的形状与①中的相同;即可得出结论.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=4,AC⊥BD,
①当BM≤4时,
∵点P′与点P关于BD对称,
∴P′P⊥BD,
∴P′P∥AC,
∴△P′BP∽△CBA,
∴$\frac{PP′}{AC}=\frac{BM}{OB}$,即$\frac{PP′}{6}=\frac{x}{4}$,
∴PP′=$\frac{3}{2}$x,
∵OM=4-x,
∴△OPP′的面积y=$\frac{1}{2}$PP′•OM=$\frac{1}{2}$×$\frac{3}{2}$x(4-x)=-$\frac{3}{4}$x2+3x;
∴y与x之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);
②当BM≥4时,y与x之间的函数图象的形状与①中的相同,过(4,0)和(8,0);
综上所述:y与x之间的函数图象大致为 .
.
故选:D.
点评 本题考查了动点问题的函数图象、菱形的性质、相似三角形的判定与性质、三角形面积的计算以及二次函数的运用;熟练掌握菱形的性质,根据题意得出二次函数解析式是解决问题的关键.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
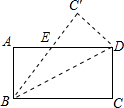 已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.
已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
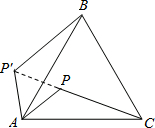 如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.
如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
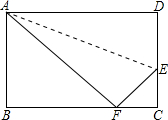 如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.
如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
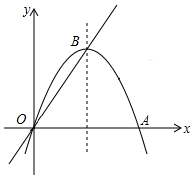 如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
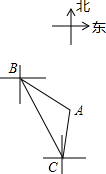 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | $\frac{20\sqrt{3}}{3}$海里 | D. | $\frac{40\sqrt{3}}{3}$海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
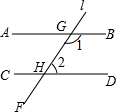 如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com