
【题目】等腰![]() 被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰
被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰![]() 的顶角的度数是____.
的顶角的度数是____.
【答案】![]() 或
或![]() 或
或![]()
【解析】
因为题中没有指明是过顶角的顶点还是过底角的顶点,且其中一个等腰三角形与原三角形相似与故应该分三种情况进行分析,从而求解.
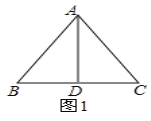
解:①如图1,∵AB=AC,当BD=CD,CD=AD,
∴∠B=∠C=∠BAD=∠CAD,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°.
此时易知∠BDA=∠BAC=90°,∠ABD=∠ABC= 45°,故![]() ∽
∽![]() ;
;
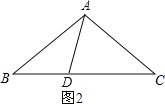
②如图2,∵AB=AC,AD=BD,AC=CD,
∴∠B=∠C=∠BAD,∠CAD=∠CDA,
∵∠CDA=∠B+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°.
此时易知∠BDA=∠BAC=108°,∠ABD=∠ABC= 36°, 故![]() ∽
∽![]() ;
;
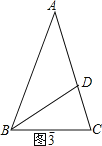
③如图3,∵AB=AC,AD=BD=BC,
∴∠B=∠C,∠BAC=∠ABD,∠BDC=∠C,
∵∠BDC=∠A+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠BAC=180°,
∴∠BAC=36°.
此时易知∠CBA=∠CDB=72°,∠BAC=∠DBC=36°,故有![]() ∽
∽![]() ;
;
故答案为:![]() 或
或![]() 或
或![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题作如下探究:
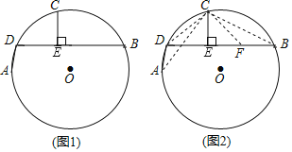
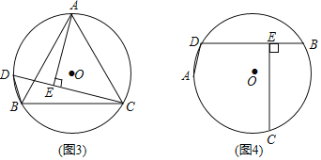
(问题发现)如图1,AD,BD为⊙O的两条弦(AD<BD),点C为![]() 的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.
的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.
(问题探究)小明同学的思路是:如图2,在BE上截取BF=AD,连接CA,CB,CD,CF.……请你按照小明的思路完成上述问题的证明过程.
(结论运用)如图3,△ABC是⊙O的内接等边三角形,点D是![]() 上一点,∠ACD=45°,连接BD,CD,过点A作AE⊥CD,垂足为E.若AB=
上一点,∠ACD=45°,连接BD,CD,过点A作AE⊥CD,垂足为E.若AB=![]() ,则△BCD的周长为 .
,则△BCD的周长为 .
(变式探究)如图4,若将(问题发现)中“点C为![]() 的中点”改为“点C为优弧
的中点”改为“点C为优弧![]() 的中点”,其他条件不变,上述结论“BE=DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE、AD、DE之间的新等量关系,并加以证明.
的中点”,其他条件不变,上述结论“BE=DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE、AD、DE之间的新等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() ),连接
),连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,探究线段
顺时针旋转,探究线段![]() 与
与![]() 的数量关系.
的数量关系.
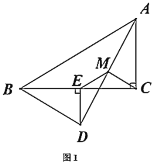
(1)如图1,点![]() 落在
落在![]() 边上时,探究
边上时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
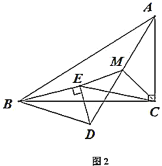
(2)如图2,点![]() 落在
落在![]() 内部时,探究
内部时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春节来临之际,小杨的服装小店用2500元购进了一批时尚围巾,上市后很快售完,小杨又用8400元购进第二批这种围巾,所购数量是第一批购进数量的3倍,但每条围巾的进价多了3元.
(1)小杨两次共购进这种围巾多少条?
(2)如果这两批围巾每条的售价相同,且全部售完后总利润率不低于20%,那么每条围巾的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王辉在某景区经营一个小摊位,他以10元/根的价格购进一批登山杖,经市场调查发现当售价为24元/根时,每天可出售156根,此后售价每增加5元,就会少售出30根.
(1)求登山杖的单根售价![]() (元)与销售数量
(元)与销售数量![]() (根)之间的函数关系式;
(根)之间的函数关系式;
(2)若设王辉每天的日销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)为了避免恶性竞争且保障商家获得一定利润,景区管理处规定登山杖的销售单价不得低于32元且不高于36元,则王辉的日销售利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() )销售量为
)销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①与
.该超市根据以往的销售经验得出以下的销售规律:①与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)![]() 与
与![]() 的关系式为________;
的关系式为________;
(2)当![]() 时,求第几天的销售利润
时,求第几天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若在当天销售价格的基础上涨![]() 元/
元/![]() ,在第
,在第![]() 天至
天至![]() 天销售利润最大值为
天销售利润最大值为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
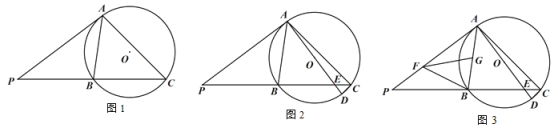
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,众志成城,举国上下,共克时艰.为确定应对疫情影响稳外贸稳外资的新举措,国务院总理李克强 3 月 10 日主持召开国务院常务会议,要求更好发挥专项再贷款再贴 现政策作用,支持疫情防控保供和企业纾困发展.会议指出,近段时间,有关部门按照国务 院要求,引导金融机构实施![]() 亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据
亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据![]() 亿元用科学记数法表示为( )
亿元用科学记数法表示为( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com