
【题目】王辉在某景区经营一个小摊位,他以10元/根的价格购进一批登山杖,经市场调查发现当售价为24元/根时,每天可出售156根,此后售价每增加5元,就会少售出30根.
(1)求登山杖的单根售价![]() (元)与销售数量
(元)与销售数量![]() (根)之间的函数关系式;
(根)之间的函数关系式;
(2)若设王辉每天的日销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)为了避免恶性竞争且保障商家获得一定利润,景区管理处规定登山杖的销售单价不得低于32元且不高于36元,则王辉的日销售利润最大是多少元?
【答案】(1)y=-6x+300;(2)W=-6![]() +2400;(3)当售价定为32元时,王辉的日销售利润最大,且最大利润为2376元.
+2400;(3)当售价定为32元时,王辉的日销售利润最大,且最大利润为2376元.
【解析】
(1)根据销售单价和销售量之间的关系,列出函数关系式y=156-![]() 化简即可;
化简即可;
(2)根据日销售利润=单根利润×数量,可得出函数关系式W=-6![]() +2400,化简整理即可;
+2400,化简整理即可;
(3)由(2)中结论,利用二次函数的最值问题,结合单价的取值范围,即可求出结果.
(1)依据题意得,y与x的函数关系式为:y=156-![]() ,
,
整理,得y=-6x+300,
答:所求y与x的函数关系式为:y=-6x+300,
故答案为:y=-6x+300;
(2)依据日销售利润=单根利润×数量,得W与x的函数关系式为:W=(x-10)(-6x+300),
整理得W=-6![]() +2400,
+2400,
答:日销售利润W和x的函数关系式为:W=-6![]() +2400,
+2400,
故答案为:W=-6![]() +2400;
+2400;
(3)∵W=-6![]() +2400,a=-6<0,
+2400,a=-6<0,
∴x>30,W随x的增加而减小,
∵销售单价不得低于32元且不高于36元,
∴当x=32时,W有最大值,且最大值为W=-6![]() +2400=2376(元),
+2400=2376(元),
答:当售价定为32元时,王辉的日销售利润最大,且最大利润为2376元,
故答案为:2376.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
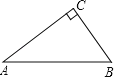
(1)以AB边上一点O为圆心作⊙O,使⊙O经过点A,C;(保留作图痕迹,不写作法)
(2)判断点B与⊙O的位置关系是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏参加答题游戏,答对最后两道单选题就顺利通关.第一道单选题有3个选项![]() ,
,![]() ,
,![]() ,第二道单选题有4个选项
,第二道单选题有4个选项![]() ,
,![]() ,
,![]() ,
,![]() ,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是
,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是![]() ,第二道题的正确选项是
,第二道题的正确选项是![]() ,解答下列问题:
,解答下列问题:
(1)如果小敏第一道题不使用“求助”,那么她答对第一道题的概率是________;
(2)如果小敏将“求助”留在第二道题使用,用画树状图或列表的方法,求小敏顺利通关的概率;
(3)小敏选第________道题(选“一”或“二”)使用“求助”,顺利通关的可能性更大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鲁在一个不透明的盒子里装了5个除颜色外其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣x+3交x轴于点B,交y轴于点A,过点A作AC⊥AB交x轴于点C.
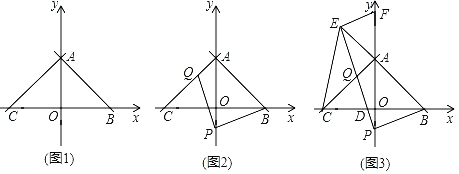
(1)如图1,求直线AC的解析式;
(2)如图2,点P在AO的延长线上,点Q在AC上,连接PB,PQ,且PQ=PB,设点P的纵坐标为t,AQ的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,PQ交x轴于点D,延长PQ交BA的延长线于点E,过点E作EF⊥PE交y轴于点F,若DE=![]() EF,求点Q的坐标.
EF,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
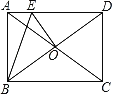
【题目】如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,∠ABE=![]() ∠ACB,若AE=2,则OE的长为_____.
∠ACB,若AE=2,则OE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
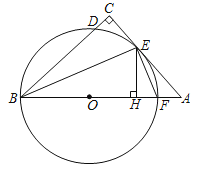
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com