
°æƒø°ø“—÷™£∫‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„OŒ™◊¯±Í‘≠µ„£¨÷±œþy£Ω©Åx+3Ωªx÷·”⁄µ„B£¨Ωªy÷·”⁄µ„A£¨π˝µ„A◊˜AC°ÕABΩªx÷·”⁄µ„C£Æ
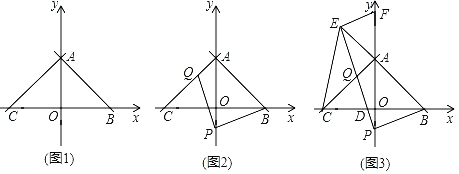
£®1£©»ÁÕº1£¨«Û÷±œþACµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº2£¨µ„P‘⁄AOµƒ—”≥§œþ…œ£¨µ„Q‘⁄AC…œ£¨¡¨Ω”PB£¨PQ£¨«“PQ£ΩPB£¨…˵„Pµƒ◊ð◊¯±ÍŒ™t£¨AQµƒ≥§Œ™d£¨«Ûd”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£®≤ª“™«Û–¥≥ˆ◊‘±‰¡øtµƒ»°÷µ∑∂Œß£©£ª
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨PQΩªx÷·”⁄µ„D£¨—”≥§PQΩªBAµƒ—”≥§œþ”⁄µ„E£¨π˝µ„E◊˜EF°ÕPEΩªy÷·”⁄µ„F£¨»ÙDE£Ω![]() EF£¨«Ûµ„Qµƒ◊¯±Í£Æ
EF£¨«Ûµ„Qµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©ACµƒΩ‚Œˆ ΩŒ™y£Ωx+3£ª£®2£©d£Ω©Å![]() t£ª£®3£©£®©Å1£¨2£©
t£ª£®3£©£®©Å1£¨2£©
°æΩ‚Œˆ°ø
£®1£©œ»∏˘æð÷±œþ![]() «Û≥ˆµ„A°¢Bµƒ◊¯±Í£¨¥”∂¯ø…µ√OA°¢OBµƒ≥§£¨‘Ÿ∏˘æðµ»—¸÷±Ω«»˝Ω«–Œµƒ≈–∂®”Ζ‘÷ µ√≥ˆOCµƒ≥§£¨¥”∂¯ø…µ√µ„Cµƒ◊¯±Í£¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«ÛΩ‚º¥ø…£ª
«Û≥ˆµ„A°¢Bµƒ◊¯±Í£¨¥”∂¯ø…µ√OA°¢OBµƒ≥§£¨‘Ÿ∏˘æðµ»—¸÷±Ω«»˝Ω«–Œµƒ≈–∂®”Ζ‘÷ µ√≥ˆOCµƒ≥§£¨¥”∂¯ø…µ√µ„Cµƒ◊¯±Í£¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«ÛΩ‚º¥ø…£ª
£®2£©œ»«Û≥ˆµ„Pµƒ◊¯±Í£¨‘Ÿ∏˘æðAQµƒ≥§°¢÷±œþACµƒΩ‚Œˆ Ωø…«Û≥ˆµ„Qµƒ◊¯±Í£¨»ª∫Û∏˘æð![]() £¨¿˚”√¡Ωµ„÷ƺ‰µƒæý¿Îπ´ ΩΩ®¡¢µ» Ω«ÛΩ‚º¥ø…£ª
£¨¿˚”√¡Ωµ„÷ƺ‰µƒæý¿Îπ´ ΩΩ®¡¢µ» Ω«ÛΩ‚º¥ø…£ª
£®3£©»ÁÕº£®º˚Ω‚Œˆ£©£¨œ»«Û≥ˆµ„Qµƒ◊¯±Í£¨¥”∂¯µ√≥ˆPN°¢QNµƒ≥§£¨‘Ÿ∏˘æð’˝«–»˝Ω«–Œ∫Ø ˝÷µ°¢π¥π…∂®¿Ìµ√≥ˆDPµƒ≥§∫Õ![]() £¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œþPQµƒΩ‚Œˆ Ω£¨¡™¡¢÷±œþABµƒΩ‚Œˆ Ω«Û≥ˆµ„Eµƒ◊¯±Í£¨◊Ó∫Û¿˚”√¡Ωµ„÷ƺ‰µƒæý¿Îπ´ Ω«Û≥ˆDEµƒ≥§£¨¥˙»Î«ÛΩ‚º¥ø…£Æ
£¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œþPQµƒΩ‚Œˆ Ω£¨¡™¡¢÷±œþABµƒΩ‚Œˆ Ω«Û≥ˆµ„Eµƒ◊¯±Í£¨◊Ó∫Û¿˚”√¡Ωµ„÷ƺ‰µƒæý¿Îπ´ Ω«Û≥ˆDEµƒ≥§£¨¥˙»Î«ÛΩ‚º¥ø…£Æ
£®1£©°þ![]() Ωªx÷·”⁄µ„B£¨Ωªy÷·”⁄µ„A
Ωªx÷·”⁄µ„B£¨Ωªy÷·”⁄µ„A
¡Ó![]() £¨‘Ú
£¨‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√![]()
°ý![]()
¡Ó![]() £¨‘Ú
£¨‘Ú![]()
°ý![]()
°þ![]() £¨
£¨
°ý![]()
°þ![]()
![]()
°ý![]()
![]()
°ý![]()
…ËACµƒΩ‚Œˆ ΩŒ™![]()
Ω´µ„![]() £¨
£¨![]() ¥˙»Îµ√
¥˙»Îµ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]()
‘Ú÷±œþACµƒΩ‚Œˆ ΩŒ™![]() £ª
£ª
£®2£©°þµ„P‘⁄AOµƒ—”≥§œþ…œ£¨µ„Pµƒ◊ð◊¯±ÍŒ™t
°ý![]() £¨
£¨![]()
»ÁÕº£¨π˝µ„Q◊˜![]() ÷·Ωª”⁄µ„M
÷·Ωª”⁄µ„M
°þAQµƒ≥§Œ™![]() £¨
£¨![]()
°ý![]()
°ý![]()
°þ![]()
°ý![]()
’˚¿Ìµ√![]()
Ω‚µ√![]() ªÚ
ªÚ![]() £®…·»•£©
£®…·»•£©
π d”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™![]() £ª
£ª
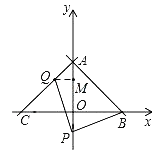
£®3£©»ÁÕº£¨π˝µ„Q◊˜![]() ÷·Ωª”⁄µ„N£¨‘Ú
÷·Ωª”⁄µ„N£¨‘Ú![]()
°þ![]()
![]()
°ý![]() £¨
£¨![]()
°ý![]()
°ý![]() £¨º¥
£¨º¥![]()
°ý![]()
°ý![]() £¨
£¨![]()
°þ![]()
°ý![]()
![]()
![]()
°ý![]()
°ý![]()
…Ë÷±œþPQµƒΩ‚Œˆ ΩŒ™![]()
Ω´µ„![]() ¥˙»Îµ√
¥˙»Îµ√![]() £¨Ω‚µ√
£¨Ω‚µ√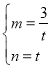
‘Ú÷±œþPQµƒΩ‚Œˆ ΩŒ™![]()
¡™¡¢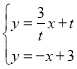 £¨Ω‚µ√
£¨Ω‚µ√![]()
°ý![]()
![]()
”…¡Ωµ„÷ƺ‰µƒæý¿Îπ´ Ωµ√£∫![]()
Ω´DE°¢DPµƒ÷µ¥˙»Î![]() µ√£∫
µ√£∫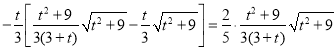
’˚¿Ìµ√£∫![]()
Ω‚µ√![]() ªÚ
ªÚ![]() £®≤ª∑˚“‚£¨…·»•£©
£®≤ª∑˚“‚£¨…·»•£©
![]() £Æ
£Æ




| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨°—O1∫Õ°—O2œýΩª”⁄A°¢B¡Ωµ„£¨ °—O1æ≠π˝µ„O2£¨µ„C‘⁄![]() …œ‘À∂Ø£®µ„C ≤ª”ÎA°¢B÷ÿ∫œ£©£¨ACµƒ—”≥§œþΩª°—O2”⁄P£¨¡¨Ω·AB°¢BC°¢BP£ª
…œ‘À∂Ø£®µ„C ≤ª”ÎA°¢B÷ÿ∫œ£©£¨ACµƒ—”≥§œþΩª°—O2”⁄P£¨¡¨Ω·AB°¢BC°¢BP£ª
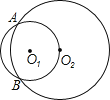
£®1£©∞¥Ã‚“‚Ω´Õº–Œ≤π≥‰ÕÍ’˚£ª
£®2£©µ±µ„C‘⁄![]() …œ‘À∂Ø ±£¨Õº÷–≤ª±‰µƒΩ«”– £®Ω´∑˚∫œ“™«ÛµƒΩ«∂º–¥…œ£©
…œ‘À∂Ø ±£¨Õº÷–≤ª±‰µƒΩ«”– £®Ω´∑˚∫œ“™«ÛµƒΩ«∂º–¥…œ£©
£®3£©œþ∂ŒBC°¢PCµƒ≥§∂»¥Ê‘⁄∫Œ÷÷πÿœµ£ø–¥≥ˆΩ·¬€£¨≤¢º”“‘÷§√˜£ª
£®4£©…Ë°—O1∫Õ°—O2µƒ∞Îæ∂Œ™![]() °¢
°¢![]() £¨µ±
£¨µ±![]() £¨
£¨![]() ¬˙◊„ ≤√¥Ãıº˛ ±£¨
¬˙◊„ ≤√¥Ãıº˛ ±£¨![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£ø
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
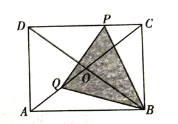
°æƒø°ø»ÁÕº£¨æÿ–Œ![]() ÷–£¨∂‘Ω«œþ
÷–£¨∂‘Ω«œþ![]() £¨
£¨![]() œýΩª”⁄µ„
œýΩª”⁄µ„![]() £¨«“
£¨«“![]() £¨
£¨![]() £Æ∂ص„
£Æ∂ص„![]() £¨
£¨![]() ∑÷±¥”µ„
∑÷±¥”µ„![]() £¨
£¨![]() Õ¨ ±≥ˆ∑¢£¨‘À∂ØÀŸ∂»æ˘Œ™lcm/s£Æµ„
Õ¨ ±≥ˆ∑¢£¨‘À∂ØÀŸ∂»æ˘Œ™lcm/s£Æµ„![]() —ÿ
—ÿ![]() ‘À∂Ø£¨µΩµ„
‘À∂Ø£¨µΩµ„![]() Õ£÷π£Æµ„
Õ£÷π£Æµ„![]() —ÿ
—ÿ![]() ‘À∂Ø£¨µ„
‘À∂Ø£¨µ„![]() µΩµ„
µΩµ„![]() Õ£¡Ù4
Õ£¡Ù4![]() ∫ۺÖ¯‘À∂Ø£¨µΩµ„
∫ۺÖ¯‘À∂Ø£¨µΩµ„![]() Õ£÷π£Æ¡¨Ω”
Õ£÷π£Æ¡¨Ω”![]() £¨
£¨![]() £¨
£¨![]() £¨…Ë
£¨…Ë![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £®’‚¿ÔπÊ∂®£∫œþ∂Œ «√ʪ˝Œ™0µƒ»˝Ω«–Œ£©£¨µ„
£®’‚¿ÔπÊ∂®£∫œþ∂Œ «√ʪ˝Œ™0µƒ»˝Ω«–Œ£©£¨µ„![]() µƒ‘À∂Ø ±º‰Œ™
µƒ‘À∂Ø ±º‰Œ™![]() £Æ
£Æ
£®1£©«Ûœþ∂Œ![]() µƒ≥§£®”√∫¨
µƒ≥§£®”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£©£ª
µƒ¥˙ ˝ Ω±Ì æ£©£ª
£®2£©«Û![]() ±£¨«Û
±£¨«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢–¥≥ˆ
÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®3£©µ±![]() ±£¨÷±Ω”–¥≥ˆ
±£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀƒ’≈ø®∆¨£¨≥˝“ª√Ê∑÷±–¥”– ˝◊÷2£¨2£¨3£¨6Õ‚£¨∆‰”ýæ˘œýÕ¨£¨Ω´ø®∆¨œ¥‘»∫Û£¨–¥”– ˝◊÷µƒ“ª√Ê≥Øœ¬ø€‘⁄◊¿√Ê…œ£¨Àʪ˙≥È»°“ª’≈ø®∆¨º«œ¬ ˝◊÷∫Û∑≈ªÿ£¨œ¥‘»∫Û»‘Ω´–¥”– ˝◊÷µƒ“ª√Ê≥Øœ¬ø€‘⁄◊¿√Ê…œ£¨‘Ÿ≥È»°“ª’≈£Æ
£®1£©”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û¡Ω¥Œ∂º«°∫√≥ȵΩ2µƒ∏≈¬ £ª
£®2£©–°±¥∫Õ–°æß“‘¥ÀŒ™”Œœ∑£¨”Œœ∑πÊ‘Ú «£∫µ⁄“ª¥Œ≥È»°µƒ ˝◊÷◊˜Œ™ ÆŒª£¨µ⁄∂˛¥Œ≥È»°µƒ ˝◊÷◊˜Œ™∏ˆŒª£¨◊È≥…“ª∏ˆ¡ΩŒª ˝£¨»Ù◊È≥…µƒ¡ΩŒª ˝≤ª–°”⁄32£¨–°±¥ªÒ §£¨∑Ò‘Ú–°æßªÒ §£Æƒ„»œŒ™’‚∏ˆ”Œœ∑π´∆Ω¬£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕº1£¨Õº2∑÷± «10°¡6µƒÕ¯∏Ò£¨Õ¯∏Ò÷–√ø∏ˆ–°’˝∑Ω–Œµƒ±þ≥§æ˘Œ™1£¨√ø∏ˆÕ¯∏Ò÷–ª≠”–“ª∏ˆ∆Ω––Àƒ±þ–Œ£¨«Î∑÷±‘⁄Õº1£¨Õº2÷–∏˜ª≠“ªÃıœþ∂Œ£¨∏˜Õºæ˘¬˙◊„“‘œ¬“™«Û£∫
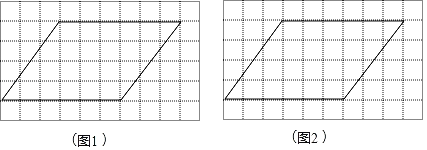
£®1£©œþ∂Œµƒ“ª∏ˆ∂Àµ„Œ™∆Ω––Àƒ±þ–Œµƒ∂•µ„£¨¡Ì“ª∏ˆ∂Àµ„‘⁄∆Ω––Àƒ±þ–Œ“ª±þµƒ∏Òµ„…œ£®√ø∏ˆ–°’˝∑Ω–Œµƒ∂•µ„æ˘Œ™∏Òµ„£©£ª
£®2£©Ω´∆Ω––Àƒ±þ–Œ∑÷∏Ó≥…¡Ω∏ˆÕº–Œ£¨∂º“™«Û∆‰÷–“ª∏ˆ «÷·∂‘≥∆Õº–Œ£¨Õº1£¨Õº2µƒ∑÷∑®≤ªœýÕ¨£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕıª‘‘⁄ƒ≥æ∞«¯æ≠”™“ª∏ˆ–°ÃØŒª£¨À˚“‘10‘™/∏˘µƒº€∏Òπ∫Ω¯“ª≈˙µ«…Ω’»£¨æ≠ –≥°µ˜≤È∑¢œ÷µ± €º€Œ™24‘™/∏˘ ±£¨√øÃÏø…≥ˆ €156∏˘£¨¥À∫Û €º€√ø‘ˆº”5‘™£¨æÕª·…Ÿ €≥ˆ30∏˘£Æ
£®1£©«Ûµ«…Ω’»µƒµ•∏˘ €º€![]() £®‘™£©”Îœ˙ € ˝¡ø
£®‘™£©”Îœ˙ € ˝¡ø![]() £®∏˘£©÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®∏˘£©÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®2£©»Ù…ËÕıª‘√øÃϵƒ»’œ˙ €¿˚»ÛŒ™![]() ‘™£¨«Û
‘™£¨«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®3£©Œ™¡À±Ð√‚∂Ò–‘æ∫’˘«“±£’œ…ú“ªÒµ√“ª∂®¿˚»Û£¨æ∞«¯πп̥¶πÊ∂®µ«…Ω’»µƒœ˙ €µ•º€≤ªµ√µÕ”⁄32‘™«“≤ª∏þ”⁄36‘™£¨‘ÚÕıª‘µƒ»’œ˙ €¿˚»Û◊Ó¥Û «∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
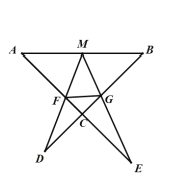
°æƒø°ø»ÁÕº£¨![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨«“
£¨«“![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨
£¨![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨¡¨
£¨¡¨![]() £¨»Ù
£¨»Ù![]() £¨‘Ú
£¨‘Ú![]() ____£Æ
____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() æ≠π˝µ„¡Ωµ„
æ≠π˝µ„¡Ωµ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨µ„
£¨µ„![]() «≈◊ŒÔœþ…œ“ª∏ˆ∂ص„£¨…˵„
«≈◊ŒÔœþ…œ“ª∏ˆ∂ص„£¨…˵„![]() µƒ∫·◊¯±ÍŒ™
µƒ∫·◊¯±ÍŒ™![]() £Æ¡¨Ω”
£Æ¡¨Ω”![]()
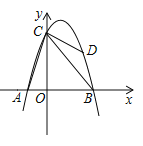
£®1£©«Û≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©µ±![]() µƒ√ʪ˝µ»”⁄
µƒ√ʪ˝µ»”⁄![]() µƒ√ʪ˝ ±£¨«Û
µƒ√ʪ˝ ±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©µ±![]() ±£¨»Ùµ„
±£¨»Ùµ„![]() «
«![]() ÷·’˝∞Î÷·…œ…œµƒ“ª∏ˆ∂ص„£¨µ„
÷·’˝∞Î÷·…œ…œµƒ“ª∏ˆ∂ص„£¨µ„![]() «≈◊ŒÔœþ…œ∂ص„£¨ ‘≈–∂œ «∑ҥʑ⁄’‚—˘µƒµ„
«≈◊ŒÔœþ…œ∂ص„£¨ ‘≈–∂œ «∑ҥʑ⁄’‚—˘µƒµ„![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£Æ»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„
Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£Æ»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„![]() µƒ◊¯±Í£∫»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£∫»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
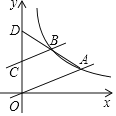
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”ÎÀ´«˙œþ
”ÎÀ´«˙œþ![]() Ωª”⁄µ„A£¨π˝µ„
Ωª”⁄µ„A£¨π˝µ„![]() ◊˜AOµƒ∆Ω––œþΩªÀ´«˙œþ”⁄µ„B£¨¡¨Ω”AB≤¢—”≥§”Îy÷·Ωª”⁄µ„
◊˜AOµƒ∆Ω––œþΩªÀ´«˙œþ”⁄µ„B£¨¡¨Ω”AB≤¢—”≥§”Îy÷·Ωª”⁄µ„![]() £¨‘Úkµƒ÷µŒ™______£Æ
£¨‘Úkµƒ÷µŒ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com