
����Ŀ����ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ�������˶��ٶȾ�Ϊlcm/s����
ͬʱ�������˶��ٶȾ�Ϊlcm/s����![]() ��
��![]() �˶�������
�˶�������![]() ֹͣ����
ֹͣ����![]() ��
��![]() �˶�����
�˶�����![]() ����
����![]() ͣ��4
ͣ��4![]() ������˶�������
������˶�������![]() ֹͣ������
ֹͣ������![]() ��
��![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ������涨���߶������Ϊ0�������Σ�����
������涨���߶������Ϊ0�������Σ�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��
��
��1�����߶�![]() �ij����ú�
�ij����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�������ʽ����д��
֮��ĺ�������ʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
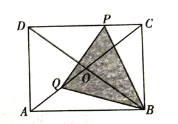
���𰸡���1����0��x��8ʱ��PD=8-x����8��x��14ʱ��PD=x-8��
��2��y= ����3��5��x��9
����3��5��x��9
��������
��1���ֵ�P���߶�CD�����߶�AD���������ηֱ���⼴�ɣ�
��2�����������Σ��ٵ�5��x��8ʱ����ͼ1�У�����y=![]() S��DPB����⼴�ɣ��ڵ�8��x��9ʱ����ͼ2�У�����y=
S��DPB����⼴�ɣ��ڵ�8��x��9ʱ����ͼ2�У�����y=![]() S��DPB����⼴�ɣ���9��x��14ʱ����ͼ3�У�����y=S��APQ+S��ABQ-S��PAB���㼴�ɣ�
S��DPB����⼴�ɣ���9��x��14ʱ����ͼ3�У�����y=S��APQ+S��ABQ-S��PAB���㼴�ɣ�
��3�����ݣ�2���н��ۼ����жϣ�
�⣺��1����0��x��8ʱ��PD=8-x��
��8��x��14ʱ��PD=x-8��
��2���ٵ�5��x��8ʱ����ͼ1�У�
���ı���ABCD�Ǿ��Σ�
��OD=OB��
��y=![]() S��DPB=
S��DPB=![]() ��
��![]() ��8-x��6=
��8-x��6=![]() ��8-x��=12-
��8-x��=12-![]() x��
x��
�ڵ�8��x��9ʱ����ͼ2�У�y=![]() S��DPB=
S��DPB=![]() ��
��![]() ��x-8����8=2x-16��
��x-8����8=2x-16��
��9��x��14ʱ����ͼ3�У�y=S��APQ+S��ABQ-S��PAB=![]() ��14-x��
��14-x��![]() ��x-4��+
��x-4��+![]() ��8��
��8��![]() ��tx-4��-
��tx-4��-![]() ��8����14-x��=-
��8����14-x��=-![]() x2+
x2+![]() x-88��
x-88��
����������y= ��
��
��3���ɣ�2����֪����5��x��9ʱ��y=![]() S��BDP��
S��BDP��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ÿ�����һСʱ����������һ���ӡ�Ϊ��ѡ�Ρ������μ䡱���Ա��ѧУ��֯���������꼶��ѡ������![]() �����Ա���б������ɼ����±���
�����Ա���б������ɼ����±���
�ɼ����֣� |
|
|
|
|
�������ˣ� |
|
|
|
|
��1���������ݵ�������______����λ����_______��
��2����֪���![]() �ֵ�ѡ���У��ߡ��ˡ����꼶�ֱ���
�ֵ�ѡ���У��ߡ��ˡ����꼶�ֱ���![]() �ˡ�
�ˡ�![]() �ˡ�
�ˡ�![]() �ˣ�ѧУ�����������ȡ������٣���ǡ�ó鵽���꼶�������Ա�ĸ��ʣ�
�ˣ�ѧУ�����������ȡ������٣���ǡ�ó鵽���꼶�������Ա�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧͼ���Ҽƻ������˼ס������ֹ����飮������7�����ֹ������4�����ֹ�������510Ԫ������3�����ֹ������5�����ֹ�������350Ԫ��
��1������ֹ���������ֹ�����ĵ��ۣ�
��2��ѧУ������ס������ֹ����鹲200�����Ҽ��ֹ�������������������ֹ������������![]() ������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μӴ�����Ϸ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��![]() ��
��![]() ��
��![]() ���ڶ�����ѡ����4��ѡ��
���ڶ�����ѡ����4��ѡ��![]() ��
��![]() ��
��![]() ��
��![]() ����������С�������ᣬ����С������һ�������������ᣬʹ�á�����������ȥ������һ�����һ������ѡ������һ�������ȷѡ����
����������С�������ᣬ����С������һ�������������ᣬʹ�á�����������ȥ������һ�����һ������ѡ������һ�������ȷѡ����![]() ���ڶ��������ȷѡ����
���ڶ��������ȷѡ����![]() ������������⣺
������������⣺
��1�����С����һ���ⲻʹ�á�����������ô����Ե�һ����ĸ�����________��
��2�����С���������������ڵڶ�����ʹ�ã��û���״ͼ���б��ķ�������С��˳��ͨ�صĸ��ʣ�
��3��С��ѡ��________���⣨ѡ��һ��������ʹ�á���������˳��ͨ�صĿ����Ը���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B=30������C=45����ADƽ����BAC��BC�ڵ�D��DE��AB������ΪE����DE=1����BC�ij�Ϊ�� ��
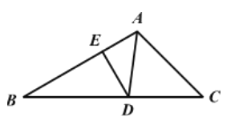
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y����x+3��x���ڵ�B����y���ڵ�A������A��AC��AB��x���ڵ�C��
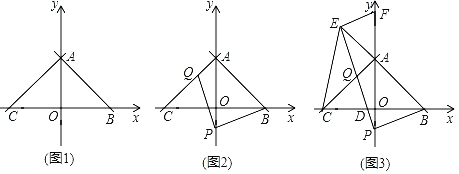
��1����ͼ1����ֱ��AC�Ľ���ʽ��
��2����ͼ2����P��AO���ӳ����ϣ���Q��AC�ϣ�����PB��PQ����PQ��PB�����P��������Ϊt��AQ�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3����ͼ3���ڣ�2���������£�PQ��x���ڵ�D���ӳ�PQ��BA���ӳ����ڵ�E������E��EF��PE��y���ڵ�F����DE��![]() EF�����Q�����꣮
EF�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
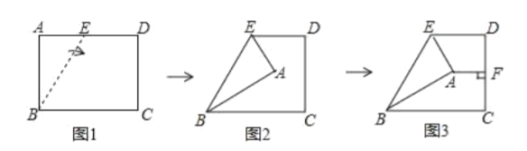
����Ŀ����ͼ 1 �ľ���![]() �У���һ��
�У���һ��![]() ��
��![]() �ϣ�����
�ϣ�����![]() Ϊ���߽���
Ϊ���߽���![]() �����ۣ���ͼ2��ʾ���ٹ���
�����ۣ���ͼ2��ʾ���ٹ���![]() ��
��![]() �ڵ�
�ڵ�![]() ����ͼ3��ʾ����
����ͼ3��ʾ����![]() �� ��ͼ3��
�� ��ͼ3��![]() �ij���Ϊ____��
�ij���Ϊ____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com