
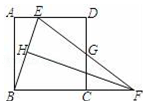
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明: ![]() =
= ![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
【答案】
(1)
证明:∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBF,
又∵FH⊥BE,
∴∠A=∠BHF=90°,
∴△ABE∽△HFB,
∴ ![]() =
= ![]()
(2)
BE2=2AEEF,
证明如下:∵∠FBE=∠FEB,
∴BF=EF,
∵FH⊥BE,
∴FH是等腰△FBE底边上的中线,
∴BH= ![]() BE,
BE,
由(1)得, ![]() ,
,
∴ ![]()
∴BE2=2AEBF;
∵BF=EF,
∴BE2=2AEEF
(3)
解:∵DG═2,
∴正方形ABCD的边长为4,
设AE=k(0<k<4),
则DE═4﹣k,BF=8﹣k,
在Rt△ABM中,BE2=AB2+AE2=16+k2,
由BE2=2AEBF,得16+k2=2k(8﹣k),
即3k2﹣16k+16=0,解得 k= ![]() 或k=4
或k=4
∵k≠4,
∴AE= ![]()
【解析】(1)根据正方形的性质得到∠AEB=∠EBF,由已知条件得到∠A=∠BHF,根据相似三角形的判定定理即可得到结论;(2)根据已知条件得到FH是等腰△FBE底边上的高,求得BH= ![]() BE,由根据相似三角形的性质得到
BE,由根据相似三角形的性质得到 ![]() ,等量代换即可得到结论;(3)由已知条件得到正方形ABCD的边长为4,设AE=k(0<k<2),则DE═4﹣k,BF=8﹣k,根据勾股定理列方程即可得到结果.
,等量代换即可得到结论;(3)由已知条件得到正方形ABCD的边长为4,设AE=k(0<k<2),则DE═4﹣k,BF=8﹣k,根据勾股定理列方程即可得到结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2018年在中央“房子是用来住的,不是用来炒”的精神作用下,房子价格持续下跌.玲玲家买了一套新房准备装修,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费为4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑应选哪家公司?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 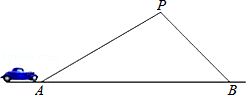
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产的一种新型节能灯,为了打开市场出台了相关政策:由厂家协调,厂家按成本价提供产品给经营户自主销售,成本价与出厂价之间的差价由厂家承担.李明按照相关政策投资销售本产品.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始销售的第一个月将销售单价定为20元,那么厂家这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么厂家为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.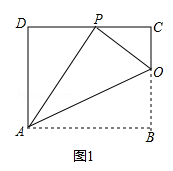
(1)求证:△HCP∽△PDA;
(2)探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com