
【题目】如图,![]() 内接于圆
内接于圆![]() ,直径
,直径![]() 的长为2,过点
的长为2,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .张老师要求添加条件后,编制一道题目,并解答.
.张老师要求添加条件后,编制一道题目,并解答.
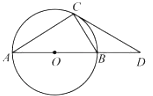
(1)在添加条件![]() ,求
,求![]() 的长,请你解答.
的长,请你解答.
(2)以下是小明,小聪的对话:
小明:我加的条件是![]() ,就可以求出
,就可以求出![]() 的长.
的长.
小聪:你这样太简单了,我加的条件是![]() ,连结
,连结![]() ,就可以证明
,就可以证明![]() 与
与![]() 全等.参考此对话,在内容中添加条件,编制一道题目(可以添线、添字母),并解答.
全等.参考此对话,在内容中添加条件,编制一道题目(可以添线、添字母),并解答.
【答案】(1)![]() ,见解析;(2)见解析.
,见解析;(2)见解析.
【解析】
(1)连接OC,如图,利用切线的性质得∠OCD=90°,再根据含30度的直角三角形三边的关系得到OD=2,然后计算OA+OD即可;
(2)添加∠DCB=30°,求AC的长,利用圆周角定理得到∠ACB=90°,再证明∠A=∠DCB=30°,然后根据含30度的直角三角形三边的关系求AC的长.
(1)连接OC,如图,

∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=30°,
∴OD=2OC=2,
∴AD=AO+OD=1+2=3;
(2)添加∠DCB=30°,求AC的长,
∵AB为直径,
∴∠ACB=90°,
∵∠ACO+∠OCB=90°,∠OCB+∠DCB=90°,
∴∠ACO=∠DCB,
∵∠ACO=∠A,
∴∠A=∠DCB=30°,
在Rt△ACB中,BC=![]() AB=1,
AB=1,
∴AC=![]() BC=
BC=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点O是对角线BD的中点.
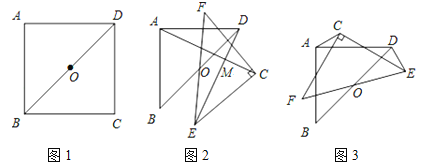
(1)观察猜想:将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是 ,直线AC与DE的位置关系是 .
(2)类比探究:将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.
(3)拓展延伸:将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
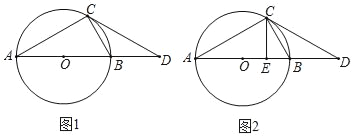
【题目】如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
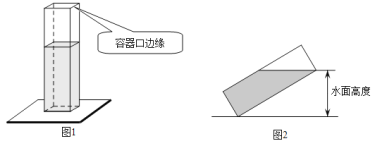
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
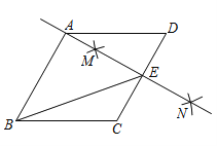
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为![]() 元/件,每天销售
元/件,每天销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(2)如果规定每天漆器笔筒的销售量不低于![]() 件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于![]() 元,试确定该漆器笔筒销售单价的范围.
元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
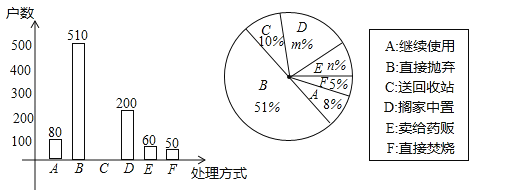
①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,分别交两条抛物线于点
轴的平行线,分别交两条抛物线于点![]() ,则以下结论:①无论
,则以下结论:①无论![]() 取何值,
取何值,![]() 的值总是正数;②
的值总是正数;②![]() ;③
;③![]() 其中正确结论是( )
其中正确结论是( )
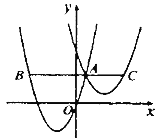
A. ①②B. ①③C. ②③D. 都正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com