
【题目】如图1,在正方形ABCD中,点O是对角线BD的中点.
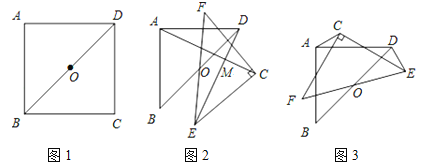
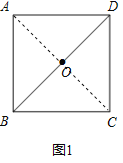
(1)观察猜想:将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是 ,直线AC与DE的位置关系是 .
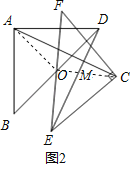
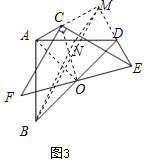
(2)类比探究:将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.
(3)拓展延伸:将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.
【答案】(1)AC=DE,AC⊥DE;(2)(1)中的结论:AC=DE,AC⊥DE仍然成立,见解析;(3)BM的最大值为![]() ﹣2,最小值为
﹣2,最小值为![]() +2.
+2.
【解析】
(1)连接OA,OC,可证△AOC≌△DOE(SAS);
(2)方法和(1)相同,易证△AOC≌△DOE(SAS);
(3)在旋转过程中,取AD中点N,连接MN,BN,BM,BM、MN、BN不共线时构成三角形,由三角形边的关系“三角形中两边之和大于第三边,两边之差小于第三边”可知:BN﹣MN<BM<BN+MN,当B,N,M共线时,
得到BM=BN+MN和BM=BN﹣MN分别为BN的最大值、最小值.
(1)如图1和图2,连接OA,OC,
∵正方形ABCD,
∴AB=BC=CD=AD,OA=OB=OC=OD,∠AOD=∠COE=90°,
∴∠AOD+∠DOC=∠COE+∠DOC,即∠AOC=∠DOE,
∴△AOC≌△DOE(SAS),
∴AC=DE,∠ACO=∠DEO,
∵∠DEO+∠EMO=90°,∠EMO=∠CMD,
∴∠ACO+∠CMD=90°,
∴AC⊥DE,
故答案为:AC=DE,AC⊥DE;
(2)(1)中的结论:AC=DE,AC⊥DE仍然成立,
如图3,连接OA,OC,延长AC,ED交于M,
∵∠AOC+∠COD=∠DOE+∠COD=90°,
∴∠AOC=∠DOE,
∵OA=OC=OD=OE,
∴△AOC≌△DOE(SAS),
∴∠OAC=∠=OCA=∠ODE=∠OED,
∵∠AOC+∠OAC+∠OCA=180°,
∴∠AOC+∠OAC+∠OED=180°,
∴∠OAC+∠AOE+∠OED=270°,
∵∠OAC+∠AOE+∠OED+∠M=360°,
∴∠M=90°,
∴AC⊥DE;
(3)如图3,取AD中点N,连接MN,BN,BM,
AB=AD=4,
在Rt△AMD中,∠AMD=90°,AN=DN,∴MN=![]() AD=
AD=![]() ×4=2,
×4=2,
在Rt△ABN中,BN=![]() ,
,
当△ECF在平面内旋转时,BN﹣MN≤BM≤BN+MN,
∴2![]() ﹣2≤BM≤2
﹣2≤BM≤2![]() +2.
+2.
∴BM的最大值为2![]() ﹣2,最小值为2
﹣2,最小值为2![]() +2.
+2.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了创建全国文明城市知识竞赛活动,初一年级全体同学参加了竞赛.收集数据:现随机抽取初一年级30名同学“创文知识竞赛”成绩,分数如下(单位:分):
90 | 85 | 68 | 92 | 81 | 84 | 95 | 93 | 87 | 89 | 78 | 99 | 89 | 85 | 97 |
88 | 81 | 95 | 86 | 98 | 95 | 93 | 89 | 86 | 84 | 87 | 79 | 85 | 89 | 82 |
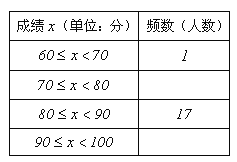

⑴请将图表中空缺的部分补充完整;
⑵学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;
⑶“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
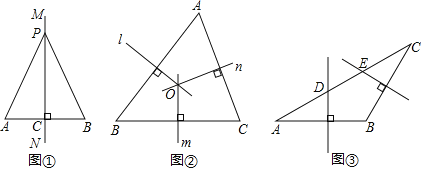
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
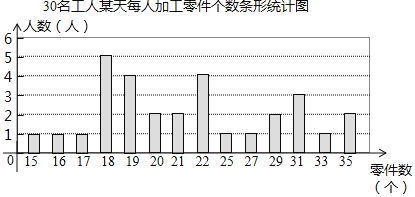
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
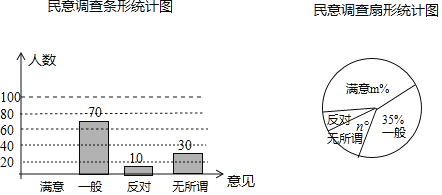
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
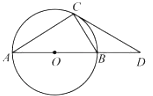
【题目】如图,![]() 内接于圆
内接于圆![]() ,直径
,直径![]() 的长为2,过点
的长为2,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .张老师要求添加条件后,编制一道题目,并解答.
.张老师要求添加条件后,编制一道题目,并解答.
(1)在添加条件![]() ,求
,求![]() 的长,请你解答.
的长,请你解答.
(2)以下是小明,小聪的对话:
小明:我加的条件是![]() ,就可以求出
,就可以求出![]() 的长.
的长.
小聪:你这样太简单了,我加的条件是![]() ,连结
,连结![]() ,就可以证明
,就可以证明![]() 与
与![]() 全等.参考此对话,在内容中添加条件,编制一道题目(可以添线、添字母),并解答.
全等.参考此对话,在内容中添加条件,编制一道题目(可以添线、添字母),并解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
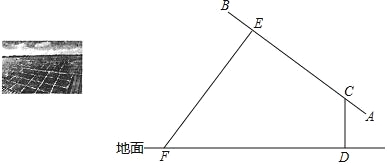
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com