
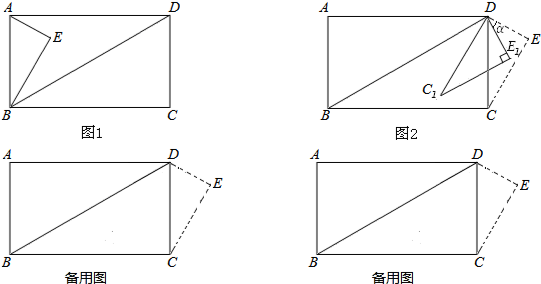
分析 (1)在Rt△ABE中,解直角三角形即可求得BE=3,进而求得BE=EE′=3,即可求得t的值;
(2)在△AED向右平移的过程中:
(I)当0≤t≤13时,如图2所示,此时重叠部分为一个三角形;
(II)当3<t≤4.5时,如图3所示,此时重叠部分为一个四边形;
(III)当4.5<t≤6时,如图4所示,此时重叠部分为一个五边形.
(3)根据旋转和等腰三角形的性质进行探究,结论是:存在α(45°或135°或90°或180°),使△BMN为等腰三角形.如图5、图6所示.
解答 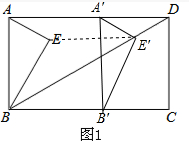 解:(1)如图1,设点E′是平移后点E落在矩形ABCD的对角线BD上的点,连接EE′,则EE′∥BC,
解:(1)如图1,设点E′是平移后点E落在矩形ABCD的对角线BD上的点,连接EE′,则EE′∥BC,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=2$\sqrt{3}$,AD=6.
在Rt△ABD中,tan∠ABD=$\frac{AD}{AB}$=$\frac{6}{2\sqrt{3}}$=$\sqrt{3}$,
∴∠ABD=60°,
∵∠ABE=30°,
∴∠EBD=30°,∠DBC=30°,
∵EE′∥BC,
∴∠EE′B=30°,
∴∠EBD=∠EE′B,
∴BE=EE′,
在Rt△ABE中,∠ABE=30°,AB=2$\sqrt{3}$,
∴BE=AB•cos30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴EE′=3,
∴t=3.
故答案为3;
(2)在△AED向右平移的过程中:
(I)当0≤t≤3时,如图2所示,此时重叠部分为△MNG,则BM=t,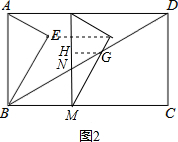
∵MN∥CD,
∴$\frac{BM}{BC}$=$\frac{MN}{CD}$,即$\frac{t}{6}$=$\frac{MN}{2\sqrt{3}}$,
∴MN=$\frac{\sqrt{3}}{3}$t,
由(1)可知BM=MG,
∴MG=t,
∵∠DBC=30°,
∴GH=$\frac{1}{2}$MG=$\frac{1}{2}$t,
∴S=$\frac{1}{2}$MN•GH=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$•$\frac{1}{2}$t=$\frac{\sqrt{3}}{12}$t2;
(II)当3<t≤4.5时,如图3所示,此时重叠部分为四边形BMKG.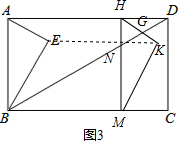
∵BM=t,∠DBC=30°,
∴MN=$\frac{\sqrt{3}}{3}$t,∠BNM=60°,
∴HN=2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t,
∵∠MHK=60°,
∴HG=NG=HN=2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t,
∴S△GHN=$\frac{1}{2}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)×$\frac{\sqrt{3}}{2}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)=$\frac{\sqrt{3}}{4}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)2
∴S=S△ABE-S△GHN=$\frac{1}{2}$×$3×\sqrt{3}$-$\frac{\sqrt{3}}{4}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)2=-$\frac{\sqrt{3}}{12}$t2+$\sqrt{3}$t-$\frac{3}{2}$$\sqrt{3}$;
(III)当4.5<t≤6时,如图4所示,此时重叠部分为五边形MHGQP.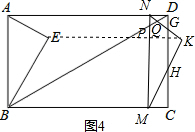
∵BM=AN=t,∴MC=ND=6-t,
∴CH=$\sqrt{3}$MC=6$\sqrt{3}$-$\sqrt{3}$t,DG=$\frac{\sqrt{3}}{3}$ND=2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t,
∵S△NPQ=$\frac{\sqrt{3}}{4}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)2,
∴S=S矩形MNDC-S△NPQ
=-S△NGD-S△MCN
=2$\sqrt{3}$(6-t)-$\frac{\sqrt{3}}{4}$(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)2-$\frac{1}{2}$(6-t)×(2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t)-$\frac{1}{2}$(6-t)×$(6\sqrt{3}$-$\sqrt{3}$t)
=-$\frac{3\sqrt{3}}{4}$t2+7$\sqrt{3}$t-15$\sqrt{3}$.
综上所述,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{12}{t}^{2}(0≤t≤3)}\\{-\frac{\sqrt{3}}{12}{t}^{2}+\sqrt{3}t-\frac{3\sqrt{3}}{2}(3<t≤4.5)}\\{-\frac{3\sqrt{3}}{4}{t}^{2}+7\sqrt{3}t-15\sqrt{3}(4.5<t≤6)}\end{array}\right.$.
(3)存在α,使△BMN为等腰三角形.
理由如下:经探究,得△BPQ∽△B1QC,
故当△BPQ为等腰三角形时,△B1QC也为等腰三角形.
(I)当BM=BN时,如图5(1),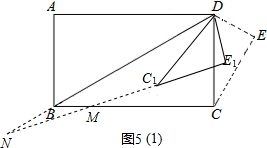
∵BM=BN,
∴∠DBC=30°,
∴∠N=∠BMN=15°,
∴∠CDE1=15°
∴α=45°;
如图5(2),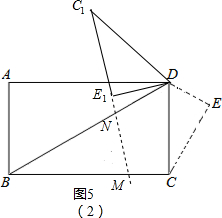
∵BM=BN,∠DBC=30°,
∴∠BNM=75°,
∴∠NDE1=15°
∴α=15°+120°=135°;
(II)当BN=MN时,如图6(1),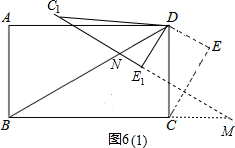
则∠DBC=∠M=30°,
∴∠DNE1=60°,
∴∠NDE1=30°,
∴∠CDE1=30°,
∴α=60°+30°=90°;
如图6(2),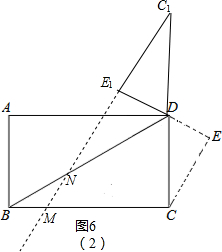
∵BM=MN,
∴∠DBC=∠MNB=30°,
∴∠NDE1=60°,
∴α=60°+60°+60°=180°;
综上所述,存在α=45°或135°或90°或180°,使△BMN为等腰三角形.
点评 本题考查了运动型与几何变换综合题,难度较大.难点在于:其一,第(2)问的运动型问题中,分析三角形的运动过程,明确不同时段的重叠图形形状,是解题难点;其二,第(3)问的存在型问题中,探究出符合题意的旋转角,并且做到不重不漏,是解题难点;其三,本题第(2)问中,计算量很大,容易失分.


科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
根据下列表格中关于x的代数式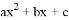 的值与x的对应值,判断方程
的值与x的对应值,判断方程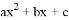 =0(a≠0,a,b,c为常数)的一个解的范围是 ( )
=0(a≠0,a,b,c为常数)的一个解的范围是 ( )
x | 5.12 | 5.13 | 5.14 | 5.15 |
| -0.04 | -0.02 | 0.01 | 0.03 |
A. 5.14<x<5.15 B. 5.13<x<5.14
C. 5.12<x<5.13 D. 5.10<x<5.12
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列方程是一元二次方程的是( )
A. x2﹣y=1 B. x2+2x﹣3=0 C. 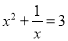 D. x﹣5y=6
D. x﹣5y=6
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.
已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对应点到旋转中心的距离相等 | B. | 图形上每一部分旋转的角度相同 | ||
| C. | 旋转前后的两个图形全等 | D. | 图形上每一点所经过的路程相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com