练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线y=-x-2交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c的顶点为A，且经过点B．

    （1）求该抛物线的解析式；

    （2）若点C（m，–）在抛物线上，求m的值．

    （3）根据图象直接写出一次函数值大于二次函数值时x 的取值范围．

    【答案】（1）抛物线解析式为 y = （x +2）2；（2）1或-5；（3）x＜﹣2 或 x＞0．

    【解析】

    （1）先利用一次函数解析式确定A、B点的坐标，然后设顶点式，利用待定系数法求抛物线解析式；

    （2）把C点坐标代入抛物线解析式得到关于m的一元二次方程，然后解方程可确定m的值；

    （3）观察函数图象，写出一次函数图象在二次函数图象上方所对应的自变量的范围即可．

    （1）当 y=0 时，﹣x﹣2=0，解得 x=﹣2，则 A（﹣2，0）， 当 x=0 时，y=﹣x﹣2=﹣2，则 B（0，﹣2），

    设抛物线解析式为 y （a x 2）2 ，

    把 B（0，﹣2）代入得 （a 0 2）2 ﹣2 ，解得 a=

    所以抛物线解析式为 y = （x +2）2

    （2）把点 C（m，）代入y = （x +2）2得（m 2）2

    解得 m1=1，m2=﹣5；

    （3）x＜﹣2 或 x＞0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】本学期学习了分式方程的解法，下面是晶晶同学的解题过程：

    解方程

    解：整理，得： …………………………第①步

    去分母，得： …………………………第②步

    移项，得： ……………………… 第③步

    合并同类项，得： ……………………… 第④步

    系数化1，得： …………………………第⑤步

    检验：当时，

    所以原方程的解是． ………………………第⑥步

    上述晶晶的解题过程从第_____步开始出现错误，错误的原因是_________________．请你帮晶晶改正错误，写出完整的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

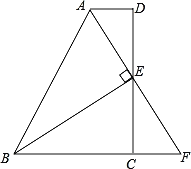
    【题目】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．

    求证：(1)FC＝AD；(2)AB＝BC+AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算：

    （2）如图，在矩形 ABCD 中，AE 平分∠BAD，交 BC 于点 E，过点 E 作 EF⊥AD 于点 F，求证：四边形ABEF 是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系内有一点A（3，4），O为坐标原点．点B在x轴上，若△AOB为等腰三角形，则点B的坐标为______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ACB＝90°．

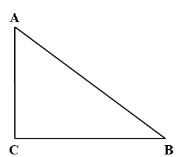
    （1）作∠BAC的平分线，交BC于点D；（要求：尺规作图，不写作法，保留作图痕迹）

    （2）在（1）的条件下，若BD＝5，CD＝3，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本小题满分9分）

    根据要求，解答下列问题．

    （1）根据要求，解答下列问题．

    ①方程x2－2x＋1＝0的解为________________________；

    ②方程x2－3x＋2＝0的解为________________________；

    ③方程x2－4x＋3＝0的解为________________________；

    …… ……

    （2）根据以上方程特征及其解的特征，请猜想：

    ①方程x2－9x＋8＝0的解为________________________；

    ②关于x的方程________________________的解为x1＝1，x2＝n．

    （3）请用配方法解方程x2－9x＋8＝0，以验证猜想结论的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，给出如下定义：已知两个函数，如果对于任意的自变量x，这两个函数对应的函数值记为y1、y2，都有点（x，y1）和（x，y2）关于点（x，x）中心对称（包括三个点重合时），由于对称中心都在直线y=x上，所以称这两个函数为关于直线y=x的特别对称函数．例如：y=x和y=为关于直线y=x的特别对称函数．

    （1）若y=3x+2和y=kx+t（k≠0）为关于直线y=x的特别对称函数，点M（1，m）是y=3x+2上一点．

    ①点M（1，m）关于点（1，1）中心对称的点坐标为　　．

    ②求k、t的值．

    （2）若y=3x+n和它的特别对称函数的图象与y轴围成的三角形面积为2，求n的值．

    （3）若二次函数y=ax2+bx+c和y=x2+d为关于直线y=x的特别对称函数．

    ①直接写出a、b的值．

    ②已知点P（﹣3，1）、点Q（2，1），连结PQ，直接写出y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围．

    查看答案和解析>>

    同步练习册答案