
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1、y2,都有点(x,y1)和(x,y2)关于点(x,x)中心对称(包括三个点重合时),由于对称中心都在直线y=x上,所以称这两个函数为关于直线y=x的特别对称函数.例如:y=![]() x和y=
x和y=![]() 为关于直线y=x的特别对称函数.
为关于直线y=x的特别对称函数.
(1)若y=3x+2和y=kx+t(k≠0)为关于直线y=x的特别对称函数,点M(1,m)是y=3x+2上一点.
①点M(1,m)关于点(1,1)中心对称的点坐标为 .
②求k、t的值.
(2)若y=3x+n和它的特别对称函数的图象与y轴围成的三角形面积为2,求n的值.
(3)若二次函数y=ax2+bx+c和y=x2+d为关于直线y=x的特别对称函数.
①直接写出a、b的值.
②已知点P(﹣3,1)、点Q(2,1),连结PQ,直接写出y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围.
【答案】(1) ①(1,﹣3);②k=﹣1,t=﹣2;(2) n=±2;(3) ①a=﹣1,b=2,c=﹣d, ②y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围为﹣8≤d<﹣3或0≤d<1
【解析】
(1)、将点代入函数解析式求出m的值,根据对称点的求法得出答案;根据特别对称函数的性质分别求出k和t的值;(2)、设y=3x+n①的特别对称函数为y=m'x+n',根据特别对称函数的性质得出m'=﹣1,n'=﹣n,则y=3x+n的特别对称函数为y=﹣x﹣n②,联立方程组求出x=﹣![]() n,y=﹣
n,y=﹣![]() n,根据面积为2求出n的值;(3)、根据特别对称函数的性质得出∴a=﹣1,b=2,c=﹣d,根据有交点分别画出两个不同的图形,从而得出答案.
n,根据面积为2求出n的值;(3)、根据特别对称函数的性质得出∴a=﹣1,b=2,c=﹣d,根据有交点分别画出两个不同的图形,从而得出答案.
(1)①∵点M(1,m)是y=3x+2上一点,∴m=5,
∴M(1,5),∴点M关于(1,1)中心对称点坐标为(1,﹣3);
②∵y=3x+2和y=kx+t(k≠0)为关于直线y=x的特别对称函数, ∴![]() =x,
=x,
∴(1+k)x+(t+2)=0, ∴k=﹣1,t=﹣2;
(2)设y=3x+n①的特别对称函数为y=m'x+n', ∴![]() =x,
=x,
∴(1+m')x+n+n'=0, ∴m'=﹣1,n'=﹣n, ∴y=3x+n的特别对称函数为y=﹣x﹣n②,
联立①②解得,x=﹣![]() n,y=﹣
n,y=﹣![]() n,
n,
∵y=3x+n和它的特别对称函数的图象与y轴围成的三角形面积为2,
∴![]() |n﹣(﹣n)|×|﹣
|n﹣(﹣n)|×|﹣![]() n|=2, ∴n=±2;
n|=2, ∴n=±2;
(3)①∵二次函数y=ax2+bx+c和y=x2+d为关于直线y=x的特别对称函数,
∴![]() , ∴(a+1)x2+(b﹣2)x+c+d=0, ∴a=﹣1,b=2,c=﹣d;
, ∴(a+1)x2+(b﹣2)x+c+d=0, ∴a=﹣1,b=2,c=﹣d;
②由①知,a=﹣1,b=2,c=﹣d, ∴二次函数y=﹣x2+2x﹣d和y=x2+d,
∴这两个函数的对称轴为直线x=1和x=0,
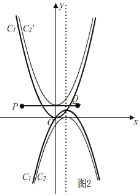
∵P(﹣3,1)、点Q(2,1),当d<0时,如图1,
当抛物线C2:y=x2+d恰好过点P(﹣3,1)时, 即:9+d=1,∴d=﹣8,
当抛物线C1:y=﹣x2+2x﹣d恰好过点Q(2,1)时, 即:﹣4+2﹣d=1,∴d=﹣3,
y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围为﹣8≤d<﹣3,
如图2,当0≤d<时,抛物线C1与线段PQ有两个交点,而抛物线C2与线段PQ没有交点,
∴y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围为0≤d<1,
即:y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围为﹣8≤d<﹣3或0≤d<1.


科目:初中数学 来源: 题型:
【题目】如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)若点C(m,–![]() )在抛物线上,求m的值.
)在抛物线上,求m的值.
(3)根据图象直接写出一次函数值大于二次函数值时x 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网两种收费方式,用户可以任选其一:A:计时制:0.05元/分;B:全月制:54元/月(限一部个人住宅电话入网).此外B种上网方式要加收通信费0.02元/分.
①某用户某月上网的时间为x小时,两种收费方式的费用分别为![]() (元)、
(元)、![]() (元),写出
(元),写出![]() 、
、![]() 与x之间的函数关系式.
与x之间的函数关系式.
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
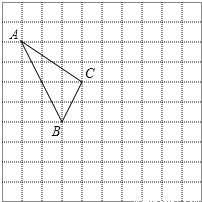
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
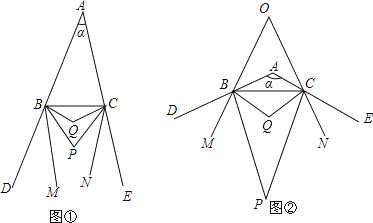
【题目】已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC= °,∠BQC= °;
(2)当α= °时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B。如图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
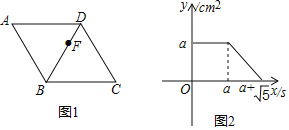
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
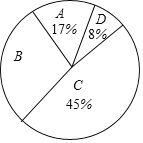
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角ΔABC中,已知AB=AC,D为底边BC上的一点,E为线段AD上的一点,且∠BED=∠BAC=2∠DEC,连接CE.
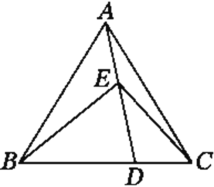
(1)求证:∠ABE=∠DAC
(2)若∠BAC=60°,试判断BD与CD有怎样的数量关系,并证明你的结论;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com