
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(m,0)、B(m+1,0)、E(2,0),其中-1≤m≤2,分别以AB、OE为边向上作正方形ABCD、OEFG.
(1)请直接写出线段AB的长;
(2)正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S,求S与m的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a,b的多项式2(a2-2ab-b2)-(a2+mab+2b2).
(1)若合并后不含有ab项,求m的值;
(2)在(1)的条件下,当a=-3,b=![]() 时,求代数式的值.
时,求代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
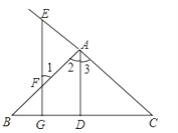
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(___________)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(_____________)
∴∠1=∠2(___________)
∠E=∠3(___________)
又∵∠E=∠1( 已知)
∴∠2=∠3(___________)
∴AD平分∠BAC(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥东起香港国际机场附近的香港口岸人工岛,向西横跨伶仃洋海域后连接珠海和澳门,止于珠海洪湾,总长 55 千米,是粤港澳三地首次合作共建的超大型跨海交通工程,也是中国第一例集桥、双人工岛、隧道为一体的通道.据统计,港珠澳大桥开通后的首个周日经大桥往来三地的车流量超过 3000辆次,客流量则接近 7.8 万人次.某天,甲乙两辆巴士均从香港口岸人工岛出发沿港珠澳大桥开往珠海洪湾,甲巴士平均每小时比乙巴士多行驶 10 千米,其行驶时间是乙巴士行驶时间的![]() 求乘坐甲巴士从香港口岸人工岛出发到珠海洪湾需要多长时间.
求乘坐甲巴士从香港口岸人工岛出发到珠海洪湾需要多长时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1,2,3,……,100这100个自然数,任意分为50组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,代入代数式![]() 中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)= ![]() .
.
例如:tan15°=tan(45°﹣30°)= ![]() =
= 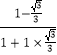 =
= ![]()
= ![]() =
= ![]() =2﹣
=2﹣ ![]() .
.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据 ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)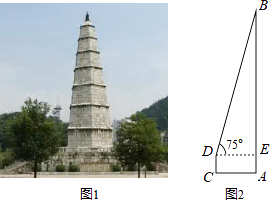
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com