
【题目】平面直角坐标系中,A(m,0)、B(m+1,0)、E(2,0),其中-1≤m≤2,分别以AB、OE为边向上作正方形ABCD、OEFG.
(1)请直接写出线段AB的长;
(2)正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S,求S与m的关系式.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
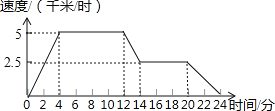
【题目】某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
速度/(千米/时) |
(2)根据图象或表格你能叙述一下小敏行走的情况吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.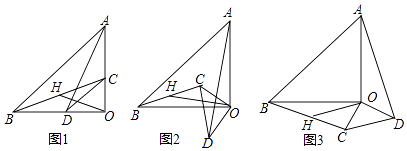
(1)如图1所示,易证:OH= ![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,3),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)直接写出B点的坐标;
(2)当点P移动了3秒时,请直接写出点P的坐标;
(3)在移动过程中,当点P到x轴距离为2个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | 0 | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| 0 | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位变化可以发现:当被开方数a每扩大100倍时,
数位变化可以发现:当被开方数a每扩大100倍时,![]() 扩大_________倍,请你利用这个规律解决下面两个问题:
扩大_________倍,请你利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ;
;
②已![]() ,若
,若![]() ,用含m的代数式表示n,则n= ;
,用含m的代数式表示n,则n= ;
(3)请根据表格提示,试比较![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x (元)的一次函数.
(1)直接写出y与x之间的函数关系式y= .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com