
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,3),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)直接写出B点的坐标;
(2)当点P移动了3秒时,请直接写出点P的坐标;
(3)在移动过程中,当点P到x轴距离为2个单位长度时,求点P移动的时间.

【答案】(1)B(4,3);(2)P(3,3);(3)点P移动的时间为1秒或4秒.
【解析】
(1)根据矩形的性质以及点的坐标的定义写出即可;
(2)先求得点P运动的距离,从而可得到点P的坐标;
(3)根据矩形的性质以及点到x轴的距离等于纵坐标的长度求出OP,再根据时间=路程÷速度列式计算即可得解.
(1)∵A点的坐标为(4,0),C点的坐标为(0,3),
∴OA=4,OC=3,
∴点B(4,3);
(2)如图所示,
∵点P移动了3秒时的距离是2×3=6,
∴点P的坐标为(3,3);
(3)点P到x轴距离为2个单位长度时,点P的纵坐标为2,
若点P在OC上,则OP=2,
t=2÷2=1秒,
若点P在AB上,则OC+BC+BP=3+4+(3﹣2)=8,
t=8÷2=4秒,
综上所述,点P移动的时间为1秒或4秒.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2020的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:横、纵坐标相等的点叫做“完美点”.
(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;
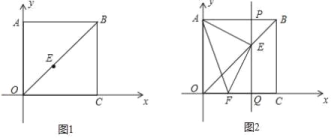
(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.
①不管t为何值,E点总是“完美点”;
②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,过E作EM∥AC交AB于点M,连结MD.
(1)当∠ADC=80°时,求∠CBE的度数.
(2)当∠ADC=α时:
①求证:BE=CE.
②求证:∠ADM=∠CDM.
③当α为多少度时,DM=![]() EM.
EM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(m,0)、B(m+1,0)、E(2,0),其中-1≤m≤2,分别以AB、OE为边向上作正方形ABCD、OEFG.
(1)请直接写出线段AB的长;
(2)正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S,求S与m的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,________
求证:________.
请你补全已知和求证
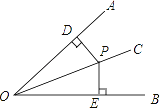
(2)并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
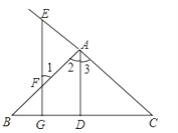
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(___________)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(_____________)
∴∠1=∠2(___________)
∠E=∠3(___________)
又∵∠E=∠1( 已知)
∴∠2=∠3(___________)
∴AD平分∠BAC(___________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com