
【题目】我们规定:横、纵坐标相等的点叫做“完美点”.
(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;
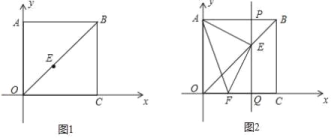
(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.
①不管t为何值,E点总是“完美点”;
②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.
【答案】(1)A(2,2);(2)①证明见解析;②当E点运动时,四边形AFQP的面积不变,面积为8.
【解析】
(1)根据“完美点”定义可求点A坐标;(2)①由题意可求直线OB的解析式y=x,点E在直线OB上移动,则可证结论;②根据题意可证△EFQ≌△APE,可求PE=FQ,则可求四边形AFQP的面积.
解(1)∵点A(x,y)是“完美点”
∴x=y
∵x+y=4
∴x=2,y=2
∴A点坐标(2,2)
(2)①∵四边形OABC是正方形,点A坐标为(0,4),
∴AO=AB=BC=4∴B(4,4)
设直线OB解析式y=kx过B点
∴4=4k,k=1
∴直线OB解析式y=x
设点E坐标(x,y)
∵点E在直线OB上移动
∴x=y
∴不管t为何值,E点总是“完美点”.
②∵E点总是“完美点”.
∴EQ=OQ
∵∠BAO=∠AOC=90°,PQ⊥x轴
∴四边形AOQP是矩形
∴AP=OQ,AO=PQ=4
∴AP=EQ
∵AE⊥EF
∴∠AEP+∠FEQ=90°,∠EAP+∠AEP=90°
∴∠FEQ=∠EAP
∵AP=EQ,∠FEQ=∠EAP,∠APE=∠EQF=90°
∴△APE≌△EFQ
∴PE=FQ
∵S四边形AFQP=![]() =2(PE+EQ)=2×PQ=8
=2(PE+EQ)=2×PQ=8
∴当E点运动时,四边形AFQP的面积不变,面积为8.


科目:初中数学 来源: 题型:
【题目】如图,线段AB的长为10cm,点D是AB上的一个动点,不与点A重合,以AD为边作等边△ACD,过点D作DP⊥CD,过DP上一动点G(不与点D重合)作矩形CDGH,对角线交于点O,连接OA、OB,则线段OB的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.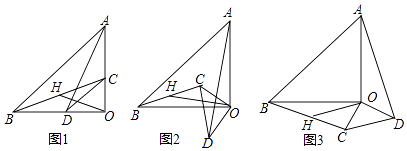
(1)如图1所示,易证:OH= ![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,3),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)直接写出B点的坐标;
(2)当点P移动了3秒时,请直接写出点P的坐标;
(3)在移动过程中,当点P到x轴距离为2个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x (元)的一次函数.
(1)直接写出y与x之间的函数关系式y= .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com