
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,过E作EM∥AC交AB于点M,连结MD.
(1)当∠ADC=80°时,求∠CBE的度数.
(2)当∠ADC=α时:
①求证:BE=CE.
②求证:∠ADM=∠CDM.
③当α为多少度时,DM=![]() EM.
EM.

【答案】(1)40°;(2)①见解析,②见解析,③60°
【解析】
(1)根据等腰三角形的性质可得∠ACD的度数,根据∠ACB=90°可求出∠BCE的度数,根据AD//BE可得∠BED=∠ADC=80°,根据三角形外角性质即可求出∠CBE的度数;(2)①由等腰三角形的性质可得∠ACD=90°-![]() ,根据∠ACB=90°可得∠BCE=
,根据∠ACB=90°可得∠BCE=![]() ,根据平行线性质可得∠BED=∠ADC=
,根据平行线性质可得∠BED=∠ADC=![]() ,利用外角性质可求出∠CBE=
,利用外角性质可求出∠CBE=![]() ,即可证明∠BCE=∠CBE,进而可证明BE=CE;②延长EM交AD于F,由EM∥AC可得
,即可证明∠BCE=∠CBE,进而可证明BE=CE;②延长EM交AD于F,由EM∥AC可得![]() ,进而可得DF=DE,AF=EC=BE,根据AAS可证明△AFM
,进而可得DF=DE,AF=EC=BE,根据AAS可证明△AFM![]() △BEM,可得FM=EM.,根据等腰三角形三线合一即可证明∠ADM=∠CDM;③由②可得DM⊥EM,由
△BEM,可得FM=EM.,根据等腰三角形三线合一即可证明∠ADM=∠CDM;③由②可得DM⊥EM,由![]() 可知tan∠DEM=
可知tan∠DEM=![]() ,可得∠DEM=60°,即可求出∠EDM=30°,进而可得
,可得∠DEM=60°,即可求出∠EDM=30°,进而可得![]() =∠ADC=2∠EDM=60°.
=∠ADC=2∠EDM=60°.
(1)∵AD=CD,∠ADC=80°,
∴∠ACD=![]() (180°-80°)=50°,
(180°-80°)=50°,
∵∠ACB=90°,
∴∠BCE=90°-50°=40°,
∵AD//BE,
∴∠BED=∠ADC=80°,
∴∠CBE=∠BED-∠BCE=80°-40°=40°.
(2)①![]() ,
,![]() ,
,
∴![]()
∵AD=CD,
∴∠ACD=![]() (180°-
(180°-![]() )=90°-
)=90°-![]() ,
,
∵∠ACB=90°,
∴∠BCE=90°-∠ACD=![]()
![]() ,
,
∴∠CBE=∠BED-∠BCE=![]()
![]() ,
,
∴∠CBE=∠BCE,
∴BE=CE.
②延长EM交AD于F
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AF=EC=BE
∵BE//AD,
∴∠FAM=∠EBM,∠AFM=∠BEM,
∴△AFM![]() △BEM
△BEM
∴FM=EM.
∴根据三线合一性可得∠ADM=∠CDM

③∵DF=DE,FM=EM,
∴DM⊥EM,
∵DM=![]() EM.
EM.
∴tan∠DEM=![]() =
=![]() ,
,
∴∠DEM=60°,
∴∠EDM=30°,
∴![]() =∠ADC=2∠EDM=60°.
=∠ADC=2∠EDM=60°.


科目:初中数学 来源: 题型:
【题目】鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售量为y个.
(1)直接写出销售量y个与降价x元之间的函数关系式;
(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣ ![]() x2+bx+c经过B、D两点.
x2+bx+c经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.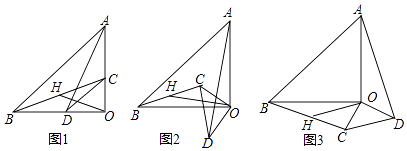
(1)如图1所示,易证:OH= ![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,3),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)直接写出B点的坐标;
(2)当点P移动了3秒时,请直接写出点P的坐标;
(3)在移动过程中,当点P到x轴距离为2个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | 0 | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| 0 | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位变化可以发现:当被开方数a每扩大100倍时,
数位变化可以发现:当被开方数a每扩大100倍时,![]() 扩大_________倍,请你利用这个规律解决下面两个问题:
扩大_________倍,请你利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ;
;
②已![]() ,若
,若![]() ,用含m的代数式表示n,则n= ;
,用含m的代数式表示n,则n= ;
(3)请根据表格提示,试比较![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
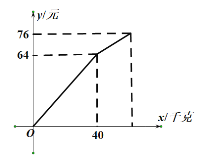
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com