
【题目】如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣ ![]() x2+bx+c经过B、D两点.
x2+bx+c经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
【答案】
(1)解:∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1、OA=OC=2,
则点B(2,1)、D(﹣1,2),代入解析式,得:
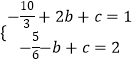 ,
,
解得: 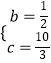 ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]()
(2)解:如图,
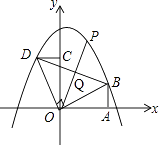
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,
∴点Q坐标为( ![]() ,
, ![]() ),
),
设直线OP解析式为y=kx,
将点Q坐标代入,得: ![]() k=
k= ![]() ,
,
解得:k=3,
∴直线OP的解析式为y=3x,
代入y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,得:﹣
,得:﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =3x,
=3x,
解得:x=1或x=﹣4,
当x=1时,y=3,
当x=﹣4时,y=﹣12,
∴点P坐标为(1,3)或(﹣4,﹣12)
【解析】(1)由旋转的性质:对应线段相等,求出B、D坐标,代入解析式即可;(2)由旋转性质知OB=OD,直线OP把△BOD的周长分成相等的两部分,可得DQ=BQ,即点Q为BD的中点;中点坐标公式是中点横纵坐标分别是端点横纵坐标和的一半,可求出Q的坐标,求出OQ的解析式,与抛物线解析式联立可求得坐标.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂去年底积压产品a件(a>0),今年预计每月销售产品2b件(b>0),同时每月可生产出产品b件,则产品积压量y(件)与今年开工时间t(月)的关系的图象应是( )
A.  B.
B. 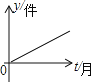 C.
C.  D.
D. 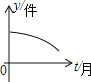
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 . 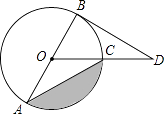
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2020的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,过E作EM∥AC交AB于点M,连结MD.
(1)当∠ADC=80°时,求∠CBE的度数.
(2)当∠ADC=α时:
①求证:BE=CE.
②求证:∠ADM=∠CDM.
③当α为多少度时,DM=![]() EM.
EM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.

(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com