
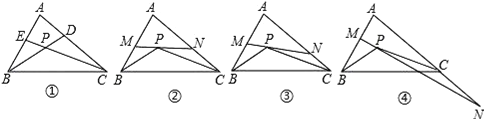
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

【答案】130°;
(2)90°﹣![]() ∠A
∠A
(3)(i)∠MPB+∠NPC=90°﹣![]() ∠A,理由见解析.
∠A,理由见解析.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣![]() ∠A.
∠A.
理由见解析.
【解析】试题分析: (1)根据三角形内角和定理得到![]() ,再根据角平分线定义得到
,再根据角平分线定义得到![]() ,再利用三角形内角和定理得
,再利用三角形内角和定理得![]() ,然后把∠A的度数代入计算;
,然后把∠A的度数代入计算;
(2)根据平角定义得![]() ,然后根据(1)的求解;
,然后根据(1)的求解;
(3)( i)∠与(2)的说理一样;
(ⅱ)有结论![]() .
.
本题解析:(1) ![]()
![]()
![]()
![]()
![]() 故答案为:
故答案为: ![]()
(2)由![]() =
= ![]() 得∠MPB+∠NPC=
得∠MPB+∠NPC=![]() ∠BPC=
∠BPC=![]() 1(
1(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A;故答案为:∠MPB+∠NPC=
∠A;故答案为:∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
(3)(i)∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
理由如下:
∵∠BPC=![]() +12∠
+12∠![]() A,
A,
∴∠MPB+∠NPC=![]() ∠BPC=180(
∠BPC=180(![]() +
+![]() ∠A)=
∠A)= ![]() 12
12![]() ∠A.
∠A.
(ii)不成立,有∠MPB∠NPC=![]()
![]() ∠A.
∠A.
理由如下:由题图④可知∠MPB+∠BPC∠NPC=![]() ,
,
由(1)知:∠BPC=![]() +
+![]() ∠A,∴∠MPB∠NPC=
∠A,∴∠MPB∠NPC=![]() ∠BPC=
∠BPC=![]() (
(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
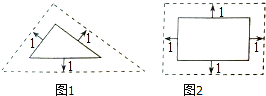
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.三角形两边之和大于第三边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=![]() ,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
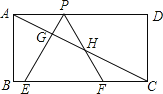
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)求证:PH﹣BE=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干张长为20厘米、宽为10厘米的长方形白纸,按图9所示的方法粘合起来,粘合部分的宽为2厘米.
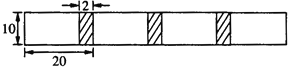
(1)求4张白纸粘合后的总长度;
(2)设x张白纸粘合后的总长度为y厘米,写出y与x之间的关系式,并求当x=20时,y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com