练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）计算：

    （2）如图，在矩形 ABCD 中，AE 平分∠BAD，交 BC 于点 E，过点 E 作 EF⊥AD 于点 F，求证：四边形ABEF 是正方形．

    【答案】（1）；（2）证明见解析.

    【解析】

    （1）根据分式的除法法则进行化简即可；

    （2）由矩形的性质得出∠FAB=∠ABE=90°，AF∥BE，证出四边形ABEF是矩形，再证明AB=BE，即可得出四边形ABEF是正方形.

    （1）原式 =

    （2）∵四边形 ABCD 是矩形，

    ∴∠FAB=∠ABE=90°，AF∥BE，

    ∵EF⊥AD，

    ∴∠FAB=∠ABE=∠AFE=90°，

    ∴四边形 ABEF 是矩形，

    ∵AE 平分∠BAD，AF∥BE，

    ∴∠FAE=∠BAE=∠AEB，

    ∴AB=BE，

    ∴四边形 ABEF 是正方形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A'的坐标是（-2，2），现将△ABC平移，使点A变换为点A'，点B'、C'分别是B、C的对应点.

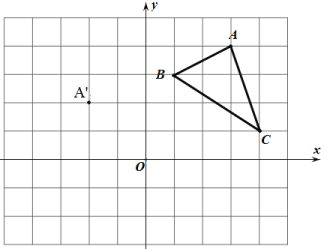
    （1）直接写出点B'、C'的坐标：B' ，C' ；并在坐标系中画出平移后的△A'B'C'（不写画法）；

    （2）若△ABC内部一点P的坐标为（a，b），则点P的对应点P的坐标是 ；

    （3）若△ABC绕点C逆时针旋转90°至△A1B1C，画出△A1B1C.

    （4）求△A'B'C'的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个抛物线型蔬菜大棚，将其横截面放在如图所示的平面直角坐标系中，抛物线可近似用函数来表示．已知大棚在地面上的宽度OA为8米，距离O点2米处的棚高BC为米．

    （1）求该抛物线的函数解析式；

    （2）若借助横梁DE建一个门，且要求门的高度不低于1.5米，则横梁DE的宽度最多是多少米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，直线与轴、轴分别交于、两点，两动点、分别以个单位长度/秒和个单位长度/秒的速度从、两点同时出发向点运动（运动到点停止）；过点作交抛物线于、两点，交于点，连结、．若抛物线的顶点恰好在上且四边形是菱形，则、的值分别为（ ）

    A. 、 B. 、 C. 、 D. 、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：(1)(2x+y)2+(x-y)(x+y)-5x(x-y)，其中x=+1，y=-1.

    (2)[(x+2y)2-(x+y)(3x-5y)-5y2]÷2x，其中x=-2，y=.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=-x-2交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c的顶点为A，且经过点B．

    （1）求该抛物线的解析式；

    （2）若点C（m，–）在抛物线上，求m的值．

    （3）根据图象直接写出一次函数值大于二次函数值时x 的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4,则等边△AEF的边长为______.

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

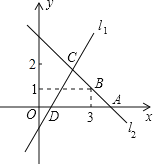
    【题目】如图，直线l1：y＝2x﹣2与x轴交于点D，直线l2：y＝kx+b与x轴交于点A，且经过点B，直线l1，l2交于点C（m，2）．

    （1）求m的值；

    （2）求直线l2的解析式；

    （3）根据图象，直接写出1＜kx+b＜2x﹣2的解集．

    （4）求△ACD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

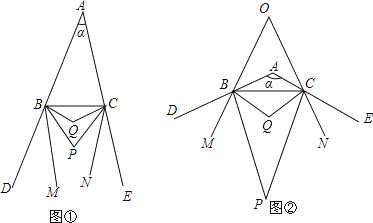
    【题目】已知如图①，BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线，BQ、CQ分别是∠PBC、∠PCB的角平分线，BM、CN分别是∠PBD、∠PCE的角平分线，∠BAC＝α．

    （1）当α＝40°时，∠BPC＝　 　°，∠BQC＝　 　°；

    （2）当α＝　 　°时，BM∥CN；

    （3）如图②，当α＝120°时，BM、CN所在直线交于点O，求∠BOC的度数；

    （4）在α＞60°的条件下，直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系：　 　．

    查看答案和解析>>

    同步练习册答案