
【题目】有一个抛物线型蔬菜大棚,将其横截面放在如图所示的平面直角坐标系中,抛物线可近似用函数![]() 来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为
来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的函数解析式;
(2)若借助横梁DE建一个门,且要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?(结果保留根号)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作答
(1)不用画图,请直接写出三角形ABC关于 x轴对称的图形三角形A1B1C1的三个顶点的坐标A1 B1 C1
(2)请画出三角形ABC关于y轴对称的三角形A’B’C’(其中 A’、B’、C’别是A、 B 、C 的对应点,不写作法)
(3)求三角形ABC的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )

A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
科目:初中数学 来源: 题型:
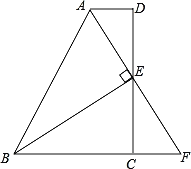
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]()
(2)如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于点 E,过点 E 作 EF⊥AD 于点 F,求证:四边形ABEF 是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
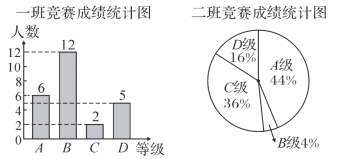
请你根据以上提供的信息解答下列问题
(1)此次竞赛中二班成绩在70分以上(包括70分)的人数为___;
(2)请你将表格补充完整:
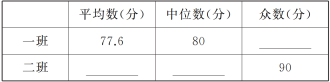
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com