
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )

A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
【答案】A
【解析】
A、设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值;B、根据函数图象判断;C、根据函数图象判断;D、设这次跳投时,球出手处离地面hm,因为(1)中求得y=﹣0.2x2+3.5,当x=﹣2,5时,即可求得结论.
解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得 3.05=a×1.52+3.5,
∴a=﹣![]() ,
,
∴y=﹣![]() x2+3.5.
x2+3.5.
故本选项正确;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
故本选项错误;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
故本选项错误;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
h=﹣0.2×(﹣2.5)2+3.5=2.25m.
∴这次跳投时,球出手处离地面2.25m.
故本选项错误.
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数![]() 的图象于点A,交函数
的图象于点A,交函数![]() 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交![]() 于点C,边接AC.
于点C,边接AC.
(1)当点P的坐标为(1,0)时,求△ABC的面积;
(2)当点P的坐标为(1,0)时,在y轴上是否存在一点Q,使A、O、Q三点为顶点的三角形△QAO为等腰三角形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(3)请你连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
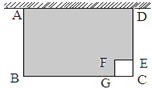
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com