
����Ŀ����ͼ����PΪx���������ϵ�һ���㣬����P��x��Ĵ��ߣ�������![]() ��ͼ���ڵ�A��������
��ͼ���ڵ�A��������![]() ��ͼ���ڵ�B������B��x���ƽ���ߣ���
��ͼ���ڵ�B������B��x���ƽ���ߣ���![]() �ڵ�C���߽�AC��
�ڵ�C���߽�AC��
��1������P������Ϊ��1��0��ʱ������ABC�������
��2������P������Ϊ��1��0��ʱ����y�����Ƿ����һ��Q��ʹA��O��Q����Ϊ�������������QAOΪ���������Σ������ڣ���ֱ��д��Q������ꣻ�������ڣ�˵�����ɣ�
��3����������OA��OC������P������Ϊ��t��0��ʱ����OAC������Ƿ���t��ֵ�ı仯���仯����˵�����ɣ�

���𰸡���1��![]() ����2����Q������Ϊ��0����
����2����Q��������0����![]() ������0��
������0��![]() ������0��2������0��1����
������0��2������0��1����
��3��������.
��������
��1������P�����������A��B�������꣬Ȼ�����C�����꣬�õ�AB=3��BC=![]() �������������������ʽ��⼴�ɣ�
�������������������ʽ��⼴�ɣ�
��2����ͼ���������OA=![]() ���ٷ�OA=OQ��AQ=AO��QO=QA����������ֱ����Q�����꼴�ɣ�
���ٷ�OA=OQ��AQ=AO��QO=QA����������ֱ����Q�����꼴�ɣ�
��3����ͼ������C��CE��x���ڵ�E��CD��y���ڵ�D����Ϊ��P������Ϊ��t��0�������Ե�A������Ϊ��t��![]() ������B��t��
������B��t��![]() ������C��
������C��![]() ��
��![]() ������ͼ����֪S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP�������ɵõ�����t�ķ��̣�Ȼ��ⷽ�̼���.
������ͼ����֪S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP�������ɵõ�����t�ķ��̣�Ȼ��ⷽ�̼���.
�⣺��1������P������Ϊ��1��0��ʱ����A��B�ĺ�����Ϊ1��
����A�ڷ���������y=![]() �ϣ���B�ڷ���������y=
�ϣ���B�ڷ���������y=![]() �ϣ�
�ϣ�
����A��1��1������B��1��4����
��BC��x�ᣬ
����C��������Ϊ4��
������C��y=![]() �ϣ�
�ϣ�
����C��������![]() ��4����
��4����
��AB=3��BC=![]() ��
��
��S��ABC=![]() ��BC��AB=
��BC��AB=![]() ��
��
��2����ͼ����ʾ��OA=![]() =
=![]() ��
��
����OA=OQ����Qλ��Q1��Q2λ�ã���ʱQ1��0����![]() ����Q2��0��
����Q2��0��![]() ����
����
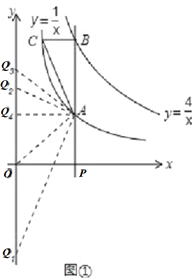
����AQ=AO����Qλ��Q3λ�ã���ʱQ3��0��2����
����QO=QA����Qλ��Q4λ�ã���ʱQ4��0��1����
��Q��������0����![]() ������0��
������0��![]() ������0��2������0��1����
������0��2������0��1����
��3������C��CE��x���ڵ�E��CD��y���ڵ�D����ͼ����ʾ��
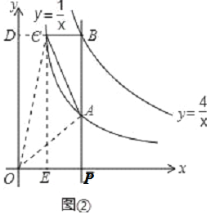
����P��������t��0����
����A��������t��![]() ������B��t��
������B��t��![]() ������C��
������C��![]() ��
��![]() ����
����
��S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP=1+![]() ��
��![]() +
+![]() ������t��
������t��![]() ����
����![]() ��
��![]() =
=![]() ��
��
����OAC���������t��ֵ�ı仯���仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P����O��ֱ��AB���ӳ����ϣ�PCΪ��O�����ߣ���CΪ�е㣬����AC������A��PC�Ĵ��ߣ���DΪ���㣬AD����O�ڵ�E��
(1)��ͼ1����֤����DAC=��PAC��
(2)��ͼ2����F�����Cλ��ֱ��AB���ࣩ����O�ϣ�![]() ������EF������F��AD��ƽ���߽�PC�ڵ�G����֤��FG=DE+DG��
������EF������F��AD��ƽ���߽�PC�ڵ�G����֤��FG=DE+DG��
(3)��(2)�������£���ͼ3����AE=![]() DG��PO=5����EF�ij���
DG��PO=5����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��AE�ǽ�ƽ���ߣ�BMƽ�֡�ABC��AE�ڵ�M������B��M����ġ�O��BC�ڵ�G����AB�ڵ�F��FBǡΪ��O��ֱ����
��1���ж�AE���O��λ�ù�ϵ����˵�����ɣ�
��2����BC=6��AC=4CEʱ�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A(8��0)��B(0��8![]() )�����ֱ��y1��ֱ��y2��
)�����ֱ��y1��ֱ��y2��![]() x+2
x+2![]() ���ڵ�C.ֱ��y2��x�ᡢy��ֱ��ڵ�D�͵�E.
���ڵ�C.ֱ��y2��x�ᡢy��ֱ��ڵ�D�͵�E.
(1)����M��A�������AB�˶����˶����ٶ���ÿ��1����λ���ȣ�����M�˶���B��ʱֹͣ�˶�����M�˶�ʱ��Ϊt�룬��ADM�����ΪS����S��t�ĺ�����ϵʽ.
(2)��y�����Ƿ���ڵ�P��ʹ��ACPΪ���������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵������.
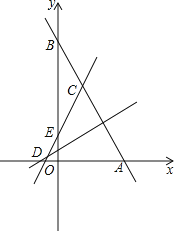
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�0��6������B�������ǣ�6��0����
��1����ͼ1����C�������ǣ���2��0����BD��AC��D��y���ڵ�E�����E�����ꣻ
��2���ڣ�1������������֤��ODƽ�֡�CDB��
��3����ͼ2����FΪAB�е㣬��GΪx�������B�Ҳ�һ���㣬����F��FG�Ĵ���FH����y��ĸ������ڵ�H����ô����G��λ�ò��ϱ仯ʱ��S��AFH��S��FBG��ֵ�Ƿ����仯������������˵�����ɣ������仯���������Ӧ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��������ͬʱ�����330ǧ�ļס�������������У�s��ǧ�ף���ʾ������صľ��룬t���֣���ʾ������ʻ��ʱ�䣬��ͼ��L1��L2�ֱ��ʾ����������s��t�Ĺ�ϵ��
��1��L1��ʾ�����������صľ�������ʻʱ��Ĺ�ϵ��
��2������B���ٶ��Ƕ��٣�
��3����L1��L2�ֱ��ʾ������������s��t�Ĺ�ϵʽ��
��4��2Сʱ������������ǧ�ף�
��5����ʻ�ʱ���A��B����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλ�����˶�Ա�ھ�����Ȧ����ˮƽ����4m������Ͷ��������һ���������˶��������˶���ˮƽ����Ϊ2.5mʱ���ﵽ���߶�3.5m��Ȼ��ȷ���������ڣ���֪��Ȧ���ľ������߶�Ϊ3.05m������ͼ��ʾ��ƽ��ֱ������ϵ�У�����˵����ȷ���ǣ�������

A. �������ߵĽ���ʽ��y=��![]() x2+3.5
x2+3.5
B. ��Ȧ���ĵ������ǣ�4��3.05��
C. �������ߵĶ��������ǣ�3.5��0��
D. �������ʱ�����ĸ߶���2m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:Rt��ABC��,��C=90��,��ABC=30��.

(1)̽��Ӧ��1:��ͼ1,Rt��ABC��,��C=90��,��ABC=30������D���߶�CB�ϣ���ADΪ�����ȱߡ�ADE������BE��Ϊ̽���߶�BE��DE֮���������ϵ���鳤�Ѿ������˸����ߣ�ȡAB���е�F������EF.�߶�BE��DE֮���������ϵ��_________,��˵�����ɣ�
(2)̽��Ӧ��2:��ͼ2,Rt��ABC��,��C=90��,��ABC=30������D���߶�CB���ӳ����ϣ���ADΪ�����ȱߡ�ADE������BE.�߶�BE��DE֮���������ϵ��__________����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB��AC����BCA��65������CD��AB��������O�ཻ�ڵ�D������BD�����DBC�Ĵ�СΪ

A. 15�� B. 35�� C. 25�� D. 45��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com