
����Ŀ����֪:Rt��ABC��,��C=90��,��ABC=30��.

(1)̽��Ӧ��1:��ͼ1,Rt��ABC��,��C=90��,��ABC=30������D���߶�CB�ϣ���ADΪ�����ȱߡ�ADE������BE��Ϊ̽���߶�BE��DE֮���������ϵ���鳤�Ѿ������˸����ߣ�ȡAB���е�F������EF.�߶�BE��DE֮���������ϵ��_________,��˵�����ɣ�
(2)̽��Ӧ��2:��ͼ2,Rt��ABC��,��C=90��,��ABC=30������D���߶�CB���ӳ����ϣ���ADΪ�����ȱߡ�ADE������BE.�߶�BE��DE֮���������ϵ��__________����˵�����ɡ�
���𰸡���1��BE=DE�����ɼ���������2��BE=DE�����ɼ�����
��������
��1���ȸ���FΪAB�е��30��ǵ�ֱ�������ε����ʵó�AC=AF�������õȱ������ε����ʺ�SAS֤����ACD�ա�AFE���ɵá�C=��AFE=90�����������߶δ�ֱƽ���ߵ����ʼ���֤�ý��ۣ�
��2����ͼ3��ȡAB���е�F������EF���£�1����˼·֤������.
(1)BE=DE.
���ɣ���ͼ1����F��AB���е㣬��AF=![]() AB.
AB.
�ߡ�C=90������ABC=30����
��AC=![]() AB����CAB=60��.
AB����CAB=60��.
��AC=AF.
�ߡ�ADE�ǵȱ������Σ�
��AD=AE=DE����EAD=60����
���CAB=��DAE��
���CAB��3=��DAE��3��
���1=��2.
�ڡ�ACD�͡�AFE�У�
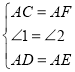 ��
��
���ACD�ա�AFE(SAS)��
���C=��AFE=90������EF��AB.
��F��AB���е㣬
��EF��AB�Ĵ�ֱƽ���ߣ�
��AE=BE��
��BE=DE.
�ʴ�Ϊ��BE=DE��
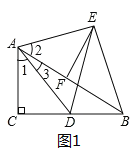
(2)BE=DE.
���ɣ���ͼ3��ȡAB���е�F������EF��
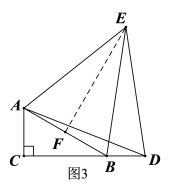
��AF=![]() AB.
AB.
�ߡ�C=90������ABC=30����
��AC=![]() AB����CAB=60��.
AB����CAB=60��.
��AC=AF.
�ߡ�ADE�ǵȱ������Σ�
��AD=AE=DE����EAD=60����
���CAB=��DAE��
���CAD=��BAE.
�ڡ�ACD�͡�AFE�У�
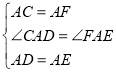 ��
��
���ACD�ա�AFE(SAS)��
���C=��AFE=90����
��EF��AB.
��F��AB���е㣬
��EF��AB�Ĵ�ֱƽ���ߣ�
��AE=BE��
��BE=DE.
�ʴ�Ϊ��BE=DE.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�C˳ʱ����ת90���õ�����FGCE����M��N�ֱ���BD��GE���е㣬��BC=14��CE=2����MN�ij���������

A. 7 B. 8 C. 9 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����PΪx���������ϵ�һ���㣬����P��x��Ĵ��ߣ�������![]() ��ͼ���ڵ�A��������
��ͼ���ڵ�A��������![]() ��ͼ���ڵ�B������B��x���ƽ���ߣ���
��ͼ���ڵ�B������B��x���ƽ���ߣ���![]() �ڵ�C���߽�AC��
�ڵ�C���߽�AC��
��1������P������Ϊ��1��0��ʱ������ABC�������
��2������P������Ϊ��1��0��ʱ����y�����Ƿ����һ��Q��ʹA��O��Q����Ϊ�������������QAOΪ���������Σ������ڣ���ֱ��д��Q������ꣻ�������ڣ�˵�����ɣ�
��3����������OA��OC������P������Ϊ��t��0��ʱ����OAC������Ƿ���t��ֵ�ı仯���仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���D��E�ֱ���AB��AC��һ�㣬��AD=AE����ABE=��ACD��BE��CD�ཻ�ڵ�F�����ж���BCF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD����AEC���ǵȱ������Σ�����BE��DC����O

(1)��֤��BE=DC ��
(2) ���DOB����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ſƼ����������˻���Ӧ��Խ��Խ�㣬��ͼ1����ijһʱ�̣����˻��ϵ�̽������ʾ�������˻�A����һ��¥����B������ǺͿ��붥��B��ͬһǦ�����ϸ�¥�ĵײ�C�ĸ��ǣ�

��1��������������븩�Ƿֱ�Ϊ30����60�����Ҹ�¥�ĸ߶�Ϊ30�ף����ʱ�����˻�����ֱ�߶�CD��
��2����ͼ2��������������븩�Ƿֱ�Ϊ���������Ҹ�¥�ĸ߶�Ϊm�ף����������¡�m��ʾ��ʱ�����˻�����ֱ�߶�CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������A��
������A��![]() ��0����B��
��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE����AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���mx2+��1��5m��x��5=0��m��0����
��1����֤������mΪ�κη���ʵ�����˷�����������ʵ������
��2����������y=mx2+��1��5m��x��5��x�ύ��A��x1��0����B��x2��0�����㣬��|x1��x2|=6����m��ֵ��
��3����m��0����P��a��b����Q��a+n��b���ڣ�2���е��������ϣ���P��Q���غϣ��������ʽ4a2��n2+8n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯һ���֪ʶ�����������涨��ÿ���༶��2��������2��Ů����1����������ʦ��ɴ����ӣ�������ʱ��ÿ��ֻ����3����Ա�ϳ���������������ʦ����μӣ�����2����Ա�ֱ���2��������2��Ů���и�������1����������1�����ɼס���2�������ͱ�����2��Ů����1������������˴����ӣ���ǡ�ó鵽�������ס�Ů��������λ������һ���ϳ������ĸ��ʣ�������������״ͼ�������б��������о����ȷ��������������̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com