
【题目】已知:如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,两动点
两点,两动点![]() 、
、![]() 分别以
分别以![]() 个单位长度/秒和
个单位长度/秒和![]() 个单位长度/秒的速度从
个单位长度/秒的速度从![]() 、
、![]() 两点同时出发向
两点同时出发向![]() 点运动(运动到
点运动(运动到![]() 点停止);过
点停止);过![]() 点作
点作![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若抛物线的顶点
.若抛物线的顶点![]() 恰好在
恰好在![]() 上且四边形
上且四边形![]() 是菱形,则
是菱形,则![]() 、
、![]() 的值分别为( )
的值分别为( )

A. ![]() 、
、![]() B.
B. ![]() 、
、![]() C.
C. ![]() 、
、![]() D.
D. ![]() 、
、![]()
【答案】A
【解析】
首先求出一次函数![]() 与坐标轴交点A、B的坐标,由EF∥AD,且EF=AD=t,则四边形ADEF为平行四边形,若平行四边形ADEF是菱形,则DE=AD=t.由DE=2OD,列方程求出t的值,进而得出G、E点坐标,求出直线BG的解析式,即可得出M点坐标,进而得出a、h的值.
与坐标轴交点A、B的坐标,由EF∥AD,且EF=AD=t,则四边形ADEF为平行四边形,若平行四边形ADEF是菱形,则DE=AD=t.由DE=2OD,列方程求出t的值,进而得出G、E点坐标,求出直线BG的解析式,即可得出M点坐标,进而得出a、h的值.
在直线解析式![]() 中,令x=0,得y=
中,令x=0,得y=![]() 3;令y=0,得x=1,
3;令y=0,得x=1,
∴A(1,0),B(0,![]() ),OA=1,OB=
),OA=1,OB=![]() ,
,
∴AB=![]() =2,
=2,
∴∠OBA=30°,
∴BF=2EF,
∵BE=![]() ,BF2=EF2+BE2,
,BF2=EF2+BE2,
∴EF=t,
∵EF∥AD,且EF=AD=t,
∴四边形ADEF为平行四边形,
若平行四边形ADEF是菱形,则DE=AD=t,
由DE=2OD,即:t=2(1-t),解得:t=![]() ,
,
∴t=![]() 时,四边形ADEF是菱形,
时,四边形ADEF是菱形,
此时BE=![]() ,则E(0,
,则E(0,![]() ),G(2,
),G(2,![]() ),
),
设直线BG的解析式为:y=kx+b,将(0,![]() ),(2,
),(2,![]() )代入得:
)代入得: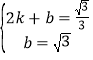 ,
,
解得: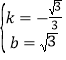 ,
,
故直线BG的解析式为:y=-![]() x+
x+![]() ,
,
当x=1时,y=![]() ,即M点坐标为(1,
,即M点坐标为(1,![]() ),
),
故抛物线y=a(x-1)2+![]() ,
,
将(0,![]() )代入得:a=-
)代入得:a=-![]() ,
,
则a、h的值分别为:![]() 、
、![]() ,
,
故选A.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 | |
50~60 | 0.39 | |
60~70 | ||
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;

(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作答
(1)不用画图,请直接写出三角形ABC关于 x轴对称的图形三角形A1B1C1的三个顶点的坐标A1 B1 C1
(2)请画出三角形ABC关于y轴对称的三角形A’B’C’(其中 A’、B’、C’别是A、 B 、C 的对应点,不写作法)
(3)求三角形ABC的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
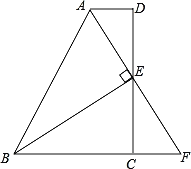
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]()
(2)如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于点 E,过点 E 作 EF⊥AD 于点 F,求证:四边形ABEF 是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°.
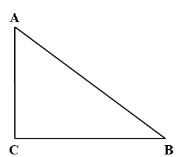
(1)作∠BAC的平分线,交BC于点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程,解应用题
甲乙两人相约周末到影院看电影,他们的家分别距离影院1200米和2000米,两人分别从家中同时出发,已知甲和乙的速度比是![]() ,结果甲比乙提前4分钟到达影院.
,结果甲比乙提前4分钟到达影院.
(1)求甲、乙两人的速度?
(2)在看电影时,甲突然接到家长电话让其15分钟内赶回家,时间紧迫改变速度,比来时每分钟多走25米,甲是否能按要求时间到家?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com