
 如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$.
如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$. 分析 此题是考查圆与正多边形结合的基本运算,空白正六边形为六个边长为2$\sqrt{3}$的正三角形,利用圆的面积公式和三角形的面积公式求得圆的面积和正六边形的面积,阴影面积=(圆的面积-正六边形的面积)×$\frac{1}{6}$.
解答 解:∵圆的半径为2$\sqrt{3}$,
∴面积为12π,
∵空白正六边形为六个边长为2$\sqrt{3}$的正三角形,
∴每个三角形面积为$\frac{1}{2}$×2$\sqrt{3}$×$2\sqrt{3}$×sin60°=3$\sqrt{3}$,
∴正六边形面积为18$\sqrt{3}$,
∴阴影面积为(12π-18$\sqrt{3}$)×$\frac{1}{6}$=2$π-3\sqrt{3}$,
故答案为:2$π-3\sqrt{3}$.
点评 本题主要考查了正多边形和圆的面积公式,注意到阴影面积=(圆的面积-正六边形的面积)×$\frac{1}{6}$是解答此题的关键.


科目:初中数学 来源: 题型:解答题
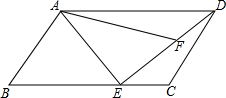 如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE;
如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC.
如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
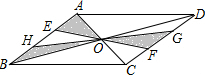 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
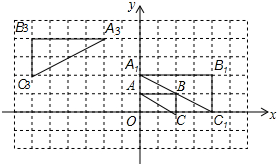 如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com